Disequazioni goniometriche elementari
Possono essere del tipo:
\[senx> m,\, \, \, \, \, senx<m,\, \, \]
\[cosx> m,\, \,\, \, \, \, cosx<m,\, \, \]
\[tanx> m,\, \, \, \, \, \, tanx<m,\, \,\]
\[cotx> m,\, \, \, \, \, \, cotx<m,\, \, \]
Per risolvere la disequazione \[senx> m\]
si deve prima di tutto risolvere $\displaystyle senx=m$ ( equazione associata ) e quindi dedurre le soluzioni della disequazione, costruendo eventualmente un grafico come mostrato nei seguenti esempi. Analogamente si procede per le altre.
Esempio 1.- Risolvere in [0°, 360°] la disequazione \[senx> \frac{1}{2}\] ( Vedi il mio video su Youtube)
Le soluzioni dell’equazione\[senx=\frac{1}{2}\]
associata alla disequazione sono \[x=30^{\circ},\, \, x=150^{\circ}\].
Pertanto le soluzioni della disequazione si deducono dal seguente grafico (fig. 1) e sono gli angoli (o archi) compresi tra P e P’ (evidenziati in rosso) ovvero: \[30^{\circ}< x< 150^{\circ}\]
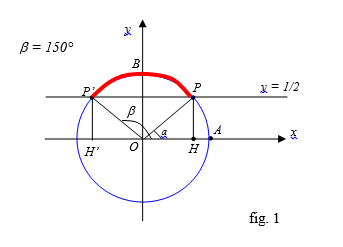
Se la disequazione fosse stata del tipo \[senx\geq \frac{1}{2}\] bisognava aggiungere alle soluzioni indicate anche le soluzioni dell’equazione associata \[x=30^{\circ},\, \, x=150^{\circ}\] e di conseguenza le soluzioni di quest’ultima disequazione sarebbero state \[30^{\circ}\leq x\leq 150^{\circ}\]
AVVERTENZA 1.- Se si voleva risolvere la disequazione dell’esempio 1 nell’insieme R dei numeri reali bisognava aggiungere la periodicità ottenendo \[x=30^{\circ}+k360^{\circ},\, \, x=150^{\circ}+k360^{\circ}\] al variare di k in Z.
Puoi consultare alcuni esercizi svolti nel mio Canale Youtube – Matematica Facile
AVVERTENZA 2.- Per una risoluzione rapida in R delle disequazioni goniometriche elementari consultare la seguente tabella:
\[sen x > m\Leftrightarrow \alpha +2k\pi <x<\pi -\alpha +2k\pi\]
\[sen x < m\Leftrightarrow (\pi -\alpha)+2k\pi <x<(2\pi -\alpha) +2k\pi\]
\[cos x > m\Leftrightarrow -\alpha+2k\pi <x<\alpha +2k\pi\]
\[cos x < m\Leftrightarrow \alpha+2k\pi <x<(2\pi -\alpha ) +2k\pi\]
\[tan x > m\Leftrightarrow \alpha+k\pi <x<\frac{\pi }{2} +k\pi\]
\[tan x < m\Leftrightarrow -\frac{\pi }{2}+k\pi <x<\alpha +k\pi\]
\[cot x > m\Leftrightarrow\, k\pi <x<\alpha +k\pi\]
\[cot x < m\Leftrightarrow\, \alpha +\pi <x<\pi+k\pi\]
\[k\in Z\]
Le soluzioni delle disequazioni nell’intervallo $\displaystyle \left [ 0,\, 2\pi \right ]$ si possono ottenere per k = 0.
Esempio 2.- Risolvere in R la disequazione $\displaystyle 2senx-\sqrt{3}>0$
Osservato che la disequazione data si può riscrivere nel seguente modo \[senx>\frac{\sqrt{3}}{2}\]
e che \[senx=\frac{\sqrt{3}}{2}\Rightarrow \alpha =\frac{\pi }{3}\] si ha
$\displaystyle \frac{\pi }{3}+2k\pi <x<\frac{2}{3}\pi +2k\pi$
AVVERTENZA 3.- Le suddette disequazioni si possono risolvere anche per via grafica utilizzando il grafico della relativa funzione goniometrica.
Esempio 3.-
