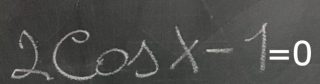Per imparare a risolvere le equazioni goniometriche conviene studiarle nel seguente ordine:
1.- Equazioni goniometriche elementari ( risoluzione in R )
$\displaystyle senx=m\Leftrightarrow x=\alpha +2k\pi ,\, \, \, x=\pi -\alpha +2k\pi,\, \, \, k\in Z$
Se k = 0 si ottengono le soluzioni nell’intervallo $\displaystyle \left [ 0,\, 2\pi \right ]$.
Si può utilizzare anche la seguente formula: \[x=\left ( -1 \right )^{k}\cdot \alpha +k\pi,\, \, \, \, con\, \, \, k\in Z\] Se k = 0 si ritrova la soluzione $\displaystyle x=\alpha$ dell’intervallo $\displaystyle \left [ 0,\, 2\pi \right ]$, mentre per k = 1 si ritrova la soluzione $\displaystyle x=\pi -\alpha$
$\displaystyle cosx=m\Leftrightarrow x=\pm \alpha +2k\pi ,\, \, \, k\in Z$
$\displaystyle tanx=p\Leftrightarrow x= \alpha +k\pi ,\, \, \, k\in Z$
$\displaystyle cotx=p\Leftrightarrow x= \alpha +k\pi ,\, \, \, k\in Z$
Le prime due equazioni sono possibili solo per \[-1\leq m\leq 1\] mentre le ultime due sono sempre possibili\[\forall p\in R\]
Esempio 1.1.- Risolvere in R le seguenti due equazioni \[cosx=\frac{\sqrt{2}}{2}, \, \, \, tanx=\frac{\sqrt{3}}{3}\]
La prima equazione è verificata per \[\alpha =45^{\circ}\] Quindi le sue soluzioni sono:
$\displaystyle x=\pm 45^{\circ}+k360^{\circ},\, \, k\in Z$
o scritto in radianti: $\displaystyle x=\pm \frac{\pi }{4}+2k\pi ,\, \, k\in Z$
La seconda equazione è verificata per \[\alpha =30^{\circ}\] Quindi le sue soluzioni sono:\[x=30+k180^{\circ},\, \, k\in Z\] o scritto in radianti: $\displaystyle x= \frac{\pi }{6}+k\pi ,\, \, k\in Z$
2.- Equazioni goniometriche elementari (risoluzione in $\displaystyle \left [ 0^{\circ},360^{\circ} \right ]\equiv \left [ 0,2\pi \right ]$ )
\[\begin{matrix} senx&=m \, \, \, \rightarrow\, \, \, x=\alpha ,x=180^{\circ}-\alpha \\ cosx&=m \, \, \, \, \rightarrow\, \, \, x=\alpha ,x=360^{\circ}-\alpha \\ tanx&=p \, \, \, \rightarrow\, \, \, x=\alpha ,x=180^{\circ}+\alpha \\ cotx&=p \, \, \, \rightarrow\, \, \, x=\alpha ,x=180^{\circ}+\alpha \end{matrix}\]
Le prime due equazioni sono possibili solo per \[-1\leq m\leq 1\] mentre le ultime due sono sempre possibili\[\forall p\in R\]
Ricordiamo che l’angolo di 180° nel sistema radiale misura $\displaystyle \pi$.
Esempio 2.1.- Risolvere in [0°, 360° ] le seguenti equazioni \[senx=\frac{\sqrt{2}}{2}, \, \, \, senx=\frac{1}{7}\]
$\displaystyle senx=-\frac{1}{2},\, \, tanx =-1,\, \, cosx=-\frac{\sqrt{2}}{2},\, \, cotx=-\sqrt{3}$
La prima equazione $\displaystyle senx=\frac{\sqrt{2}}{2}$ è verificata per $\displaystyle \alpha =45^{\circ}$, il che si vede consultando i valori fondamentali delle funzioni goniometriche (clicca qui). Quindi le sue soluzioni sono: \[x=45^{\circ},\, \, \, \, \, x=180^{\circ}-45^{\circ}=135^{\circ}\]
La seconda equazione è possibile perché 1/7 è compreso tra -1 e 1 e \[\alpha =arcsen\left ( \frac{1}{7} \right )\] Quindi le sue soluzioni sono:\[x=arcsen\left ( \frac{1}{7} \right ),\, \, x=\pi -arcsen\left ( \frac{1}{7} \right )\]
…
Qualche altro esempio? Vedi qui
Esempio 2.2.- Risolvere in R le seguenti equazioni: \[cosx=\frac{\sqrt{2}}{2}, \, \, \, tanx=\frac{\sqrt{3}}{3}\]
$\displaystyle senx=-\frac{\sqrt{3}}{2},\, \, tanx=-\sqrt{3}, \, \, cosx=-\frac{2}{5},\, \, cotx=-10\sqrt{2}$
La prima equazione è verificata per \[\alpha =45^{\circ}\] Quindi le sue soluzioni sono:\[x=45+k360^{\circ},\, \, x=315^{\circ}+k360^{\circ},\, \, \, k\in Z\]
Notiamo che in questo caso, rispetto all’esempio 1, abbiamo, come è lecito, prima risolta l’equazione nell’intervallo $\displaystyle \left [ 0^{\circ},360^{\circ} \right ]\equiv \left [ 0,2\pi \right ]$ e poi aggiunta la periodicità del coseno.
La seconda equazione è verificata per \[\alpha =30^{\circ}\] Quindi le sue soluzioni sono:\[x=30+k180^{\circ},\, \, k\in Z\]
3.- Equazioni goniometriche
\[sen\,P(x) = sen\, Q(x),\, \, \, cos\, P(x)=cos\, Q(x)\] \[tan\,P(x) = tan\, Q(x),\, \, \, cot\, P(x)=cot\, Q(x)\]
Esempio 3.1.- Risolvere in R l’equazione \[sen\left ( 75^{\circ}-2x \right )=sen\left ( x-15^{\circ} \right )\]
Esempio 3.2.- Risolvere in R l’equazione \[tan\left (- \frac{\pi }{3}+3x \right )=tan\left ( x-\frac{\pi }{10} \right )\]
Non sai risolvere l’equazione? Allora vedi il mio video su Youtube!
Esempio 3.3.- Risolvere in [0, 360°] l’equazione \[sen\, (3x)=\frac{1}{2}\]
Non sai risolvere l’equazione? Allora vedi il mio video su Youtube!
4.- Equazioni goniometriche riconducibili ad una di secondo grado
\[a\cdot sen^{2}x+b\cdot senx+c=0\]
oppure in coseno, tangente o cotangente.
Esempio 4.1.- Risolvere l’equazione \[3tan^{2}x-4\sqrt{3}tanx+3=0\]
Risoluzione
Posto tan x = y si ha l’equazione \[3y^{2}-4\sqrt{3}y+3=0\] aventi le soluzioni \[y=\frac{2\sqrt{3}\pm \sqrt{12-9}}{3}\Rightarrow y=\frac{2\sqrt{3}\pm \sqrt{3}}{3}\] ossia \[y_{1}=\frac{\sqrt{3}}{3},\, \, \, y_{2}=\sqrt{3}\]
Pertanto dalla posizione fatta si ricavano le seguenti due equazioni elementari:\[tanx=\frac{\sqrt{3}}{3},\, \, \, tanx=\sqrt{3}\]
aventi le soluzioni \[x=\frac{\pi }{6}+k\pi ,\, \, \, x=\frac{\pi }{3}+k\pi\]
con k appartenente a Z.
Esempio 4.2.- Risolvere l’equazione $\displaystyle 5sen(\pi -x)-2cos^{2}x+4=0$
Esempio 4.3.- Risolvere l’equazione $\displaystyle cos^{2}x-sen(-x)=1+sen^{2}x$
5.- Equazioni goniometriche lineari
\[asenx+bcosx=c\]
si possono risolvere in vario modo, si possono utilizzare le formule parametriche, il metodo grafico, eccetera.
Esempio 5.1.- Risolvere in R l’equazione lineare \[\sqrt{3}senx+cosx=1\]
Risoluzione
Utilizzando le formule parametriche
\[senx=\frac{2t}{1+t^{2}},\, \, cosx=\frac{1-t^{2}}{1+t^{2}},\, \, \, \, con\, \, \, t =tan\frac{x}{2}\]
si ha l’equazione razionale di secondo grado nell’incognita t:
\[\sqrt{3}\frac{2t}{1+t^{2}}+\frac{1-t^{2}}{1+t^{2}}=1\]
ossia: \[t^{2}-\sqrt{3}t=0\]
avente per soluzioni \[t=0,\, \, \, t=\sqrt{3}\]
Di conseguenza bisogna risolvere le equazioni elementari: \[tan\frac{x}{2}=0,\, \, \, tan\frac{x}{2}=\sqrt{3}\]
Posto x/2 = y si ha:
\[tan\frac{x}{2}=\sqrt{3}\Rightarrow tan\, y=\sqrt{3}\Rightarrow y=\frac{\pi }{3}+k\pi\]
e dalla posizione fatta si ricava x:\[\frac{x}{2}=\frac{\pi }{3}+k\pi \Rightarrow x=\frac{2\pi }{3}+2k\pi\]
Risolviamo anche: \[tan\frac{x}{2}=0\Rightarrow tany=0\Rightarrow y=k\pi \Rightarrow x=2k\pi\]
In definitiva le soluzioni dell’equazione assegnata sono: \[x=2k\pi\cup x=\frac{2\pi }{3}+2k\pi\]
Esempio 5.2.- Risolvere in R l’equazione lineare $\displaystyle senx+\left ( \sqrt{2} -1\right )cox-1=0$
Risoluzione ragionata
Utilizzando le formule parametriche si può ricondurre l’equazione ad una di secondo grado nell’incognita $\displaystyle t=tan\left ( \frac{x}{2} \right )$ , e tale equazione di secondo grado è a coefficienti irrazionali e bisogna utilizzare la formula di riduzione del radicale doppio, in definita si ottengono due soluzioni distinte e si è ricondotti a risolvere due equazione elementari …
Esempio 5.3.- Risolvere in R l’equazione lineare $\displaystyle sen\left ( x-\frac{\pi }{4} \right )+cos\left ( x-\frac{\pi }{4} \right )=1$
Esempio 5.4.- Risolvere in R l’equazione lineare$\displaystyle senx+3cox-7=0$
6.- Equazioni goniometriche omogenee di secondo grado (e quarto grado)
\[a\cdot sen^{2}x+b\cdot senxcosx+c\cdot cos^{2}x=d\]
Esempio 6.1.- Risolvere la seguente equazione omogenea \[\sqrt{3}\cdot senx\, cosx+cos^{2}x=1\]
Risoluzione
Utilizzando l’identità fondamentale della goniometria \[sen^{2}x+cos^{2}x=1\] l’equazione data si può riscrivere nel seguente modo:
\[\sqrt{3}\cdot senx\, cosx+cos^{2}x=sen^{2}x+cos^{2}x\]
da cui sommando i termini simili si ha:
\[\sqrt{3}\cdot senx\, cosx-sen^{2}x=0\]
e dividendo ambo i membri per cos^2(x) si ha:
\[tan^{2}x-\sqrt{3}\cdot tanx =0\]
e risolvendo tale equazione si ottengono le seguenti due equazioni elementari in tan x:
\[ tan x=0\, \cup\, tanx=\sqrt{3}\] …
Esempio 6.2.- Risolvere la seguente equazione omogenea di secondo grado:
\[2cosxsenx-cos^{2}x+sen^{2}x=0\]
Esempio 6.3.- Risolvere la seguente equazione omogenea di quarto grado:
7.- Equazioni simmetriche in sen x e cos x
\[a\cdot senxcosx+b\cdot (senx+cosx)+c=0\]
si possono risolvere con la sostituzione x = 45° + y, con y incognita ausiliaria.
Esempio 7.1.- Risolvere la seguente equazione simmetrica
4 senx cosx – 1 = 0
Risoluzione
Con la sostituzione x = 45° + y l’equazione diventa:
4 sen(45° + y) cosx(45° + y ) – 1 = 0
e sviluppando con le formule di addizione si ha:
\[ 4\left ( sen45^{\circ}cosy+senycos45^{\circ} \right )\left ( cos45^{\circ}cosy-sen45^{\circ}seny \right )-1=0\]
da cui
\[ 4\left ( \frac{\sqrt{2}}{2}cosy+seny\frac{\sqrt{2}}{2} \right )\left ( \frac{\sqrt{2}}{2}cosy-\frac{\sqrt{2}}{2}seny \right )-1=0\]
\[ 4\frac{\sqrt{2}}{2}\frac{\sqrt{2}}{2}\left ( cosy+seny \right )\left ( cosy-seny \right )-1=0\]
ossia
\[ 2\left ( cosy+seny \right )\left ( cosy-seny \right )-1=0\]
ed infine
\[ 2cos^{2}y-2sen^{2}y-1=0\]
e riducendo ad una equazione in solo seny si ha:
\[ -4sen^{2}y+1=0\]
che si riduce alle seguenti due equazioni elementari
\[ seny=\frac{1}{2}\: \cup\, seny=-\frac{1}{2}\]
La prima ammette come soluzioni
\[ y=\frac{\pi }{6}+2k\pi ,\, \, y=\frac{5\pi }{6}+2k\pi\]
e tenuto conto della posizione iniziale x = 45° + y ossia y = x – 45° si ha
\[ x-\frac{\pi }{4}=\frac{\pi }{6}+2k\pi ,\, \, x-\frac{\pi }{4}=\frac{5\pi }{6}+2k\pi\]
ossia
\[ x=\frac{\pi }{6}+\frac{\pi }{4}+2k\pi ,\, \, x=\frac{5\pi }{6}+\frac{\pi }{4}+2k\pi\]
cioè
\[x=\frac{5\pi }{12}+2k\pi ,\, \, x=\frac{13\pi }{12}+2k\pi\]
Resta da risolvere la seconda equazione goniometrica \[ seny=-\frac{1}{2}\]…
8.- Equazioni g. di vario tipo con due o più funzioni goniometriche e/o con angoli diversi
Per risolvere un’equazione di questo tipo bisogna in genere ricondurla ad un’altra con una sola funzione goniometrica e con un solo angolo o ad una dei casi precedenti grazie all’utilizzo delle formule di goniometria. In taluni casi si può trasformare l’equazione assegnata nell’unione di due o più equazioni più semplici o elementari.
Esempio 8.1.- Risolvere l’equazione $\displaystyle cos2x-sen2x\cdot tanx=0$
Esempio 8.2.- Risolvere l’equazione $\displaystyle 3sen2x+10senx=0$
Esempio 8.3.- Risolvere l’equazione $\displaystyle cos(x-\pi )+cos^{2}x=0$
Esempio 8.4.- Risolvere in R l’equazione $\displaystyle 3sen2x\, tanx-2cos^{2}x=2$
Esempio 8.5.- Risolvere in R le equazioni $\displaystyle sen^{2}2x\, -2-2cos\, 2x=0$, $\displaystyle cosx-2sen^{2}\frac{x}{2}=cos^{2}\frac{x}{2}$
Esempio 8.6.- Risolvere in R le equazioni
$\displaystyle cot\, 2x\cdot cotx=1$, $\displaystyle 2sen\left ( \frac{\pi }{6} +x\right )cosx=1$
Esempio 8.7.- Risolvere in R l’equazione \[sen2x-\sqrt{2}\left ( senx+cosx \right )+1=0\]
Non sai risolvere l’equazione? Allora vedi il mio video su Youtube!
Esempio 9. Equazione goniometrica esponenziale tratta dall’Olimpiade della Goniometria
Puoi consultare alcuni esercizi svolti nel mio Canale Youtube – Matematica Facile