- Variabile statistica (carattere): caratteristica che viene presa in esame in un certo studio statistico (esempi: altezza, età, sesso, titolo di studio, peso, colore degli occhi, reddito). Può essere discreta o continua.
- Modalità: modo di manifestarsi di una variabile statistica;
- Unità statistica: singola unità elementare su cui vengono osservati i caratteri oggetto di studio (esempi: studente, famiglia, reddito di una persona, ecc.)
- Popolazione: insieme di unità statistiche omogenee rispetto a una o più caratteristiche (esempi:studenti dell’Università di Milano, residenti nella regione Lazio, popolazione delle famiglie italiane)
Distribuzioni statistiche – Frequenze assolute e frequenze relative
Se in una popolazione formata da k elementi, una variabile discreta X assume n modalità distinte
\[\left \{ x_{1}, x_{2},…, x_{n} \right \}\]
in modo che la modalità $\displaystyle x_{1}$ si presenta $\displaystyle k_{1}$ volte, la modalità $\displaystyle x_{2}$ si presenta $\displaystyle k_{2}$ volte, … , la modalità $\displaystyle x_{n}$ si presenta $\displaystyle k_{n}$ volte, è possibile rappresentare questi dati mediante una tabella (Tab. 1) del tipo:

Tale tabella si chiama distribuzione di frequenza della variabile X, le quantità
$\displaystyle k_{i}\, \, per\, \, i=1,2,…,n$
si chiamano frequenze assolute e sono numeri interi tali che:\[\sum_{i=1}^{k}i_{k}=k,\, \, \, \, 0\leq k_{i}\leq k\] mentre le quantità $\displaystyle \frac{k_{i}}{k}$ si dicono frequenze relative e sono tali che:
$\displaystyle \sum_{i=1}^{n}\frac{k_{i}}{k}=1, \, \, con\, \, 0\leq \frac{k_{i}}{k}\leq 1$
Se la variabile X è continua allora si usa suddividere i valori assunti dalla variabile in classi di modalità riferendo la distribuzione delle frequenze agli elementi che appartengono ad una data classe. I metodi maggiormente usati per suddividere in classi i valori assunti dalla variabile X sono il metodo delle classi equi-ampie e quello delle classi equi-frequenti. In questo caso i dati si possono rappresentare come nella tabella 2.
Frequenze cumulate e funzione di ripartizione per distribuzioni discrete
Frequenze cumulate:
Numero di unità statistiche con valori di
\[X\leq x_{i}\]
\[frequenze\, \, cumulate\, \, \left ( x_{i} \right )=\sum_{k=1}^{i}n_{k}\]
Funzione di ripartizione empirica:
La funzione di ripartizione
\[F\left ( x_{i} \right )\]
di una variabile X – proporzione di unità statistiche con valori di \[X\leq x_{i}\]
è:
\[F\left ( x_{i} \right )=\sum_{k=1}^{i}f_{k}\]
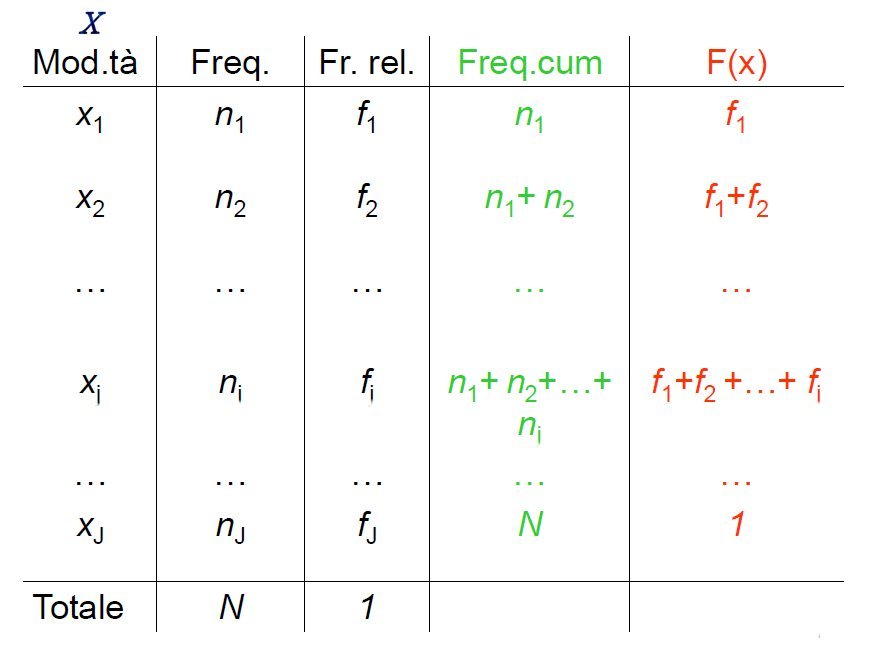
Avvertenza
Si possono costruire tabelle anche con frequenze assolute o relative cumulate o in percentuale.

