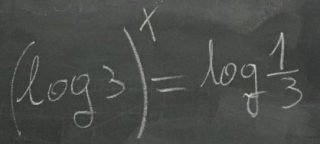
Esempio 1.1.- Risolvere le seguenti equazioni esponenziali \[2^{x+1}+2^{3-x}=17\]
La risoluzione è indicata nella seguente foto. Le soluzioni sono: x = -1, x = 3
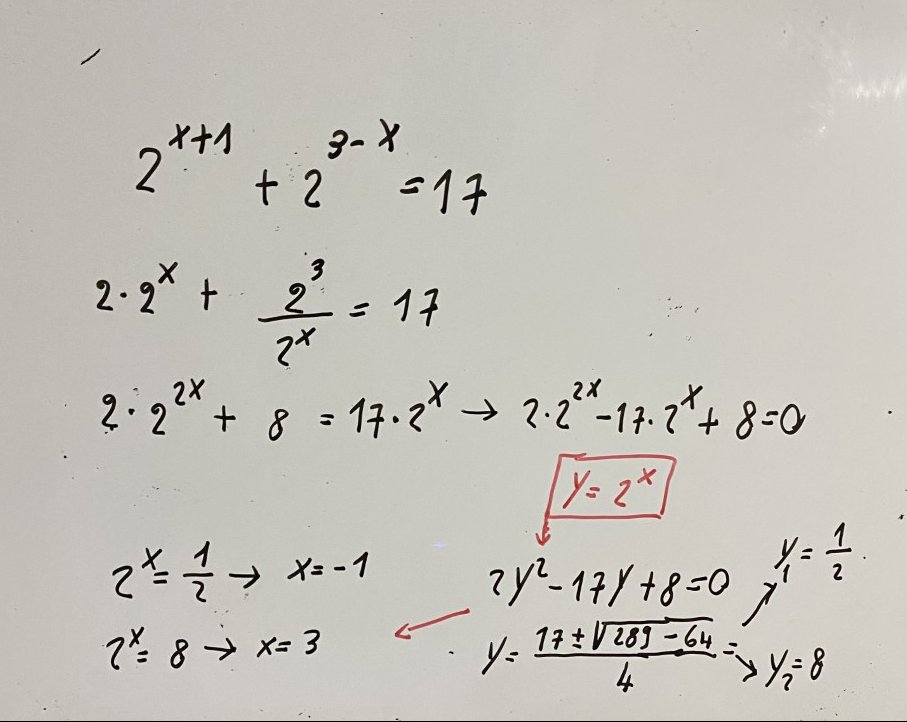
\[2^{x+3}+4^{x+1}=320\]
\[2^{x}+8=\frac{1}{4}+2^{1-x}\]
\[10^{x}+10^{2-x}=101\]
\[7^{x+1}=3^{x+1}\]
Esempio 1.2- Risolvere le seguenti equazioni esponenziali \[\sqrt{8^{x}}+4\cdot 2^{-\frac{x}{2}}=5\cdot 2^{\frac{x}{2}}\] \[7^{x-3}=4^{2x+1}\] \[2^{2+\sqrt{x}}+2^{2-\sqrt{x}}=17\]
La prima equazione ammette le soluzioni: 0, 2.
Prova risolvere la seconda o vedi il mio video su Youtube
Esempio 2.- Risolvere la seguente equazione logaritmica \[log_{3}(x+8)+log_{3}(2x+7)=log_{3}(11x+232)-log_{3}(x+2)\]
Prima di tutto richiediamo che gli argomenti dei logaritmi siano positivi. Si ha \[\left\{\begin{matrix} x+8 &>0 \\ 2x+7 &>0 \\ 11x+232& >0 \\ x+2& >0 \end{matrix}\right.\] da cui x > – 2
Quindi, sotto la condizione che x > – 2, applichiamo i teoremi sui logaritmi e si ha: \[log_{3}(x+8)(2x+7)=log_{3}\frac{11x+232}{x+2}\]
ossia \[(x+8)(2x+7)=\frac{11x+232}{x+2}\] e tolto il denominatore si ha \[(x+8)(2x+7)(x+2)=11x+232\]
da cui l’equazione di terzo grado \[2x^{3}+27x^{2}+91x-120=0\] che ammette come unica soluzione reale x = 1.
Quindi l’equazione logaritmica assegnata ammette soluzione x = 1.
Esempio 3.- Risolvere la seguene equazione esponenziale \[x^{\sqrt{x}}=\sqrt{x^{x}}\]
Trasformiamo l’equazione applicando l’identità \[f(x)^{g(x)}=e^{g(x)lnf(x)}\] e si ha:
\[x^{\sqrt{x}}=e^{\sqrt{x}lnx},\, \, \, \sqrt{x^{x}}=x^{\frac{x}{2}}=e^{\frac{x}{2}lnx}\] e quindi l’equazione assegnata diventa \[e^{\sqrt{x}lnx}=e^{\frac{x}{2}lnx}\Rightarrow \sqrt{x}lnx=\frac{x}{2}lnx\Rightarrow \left ( \sqrt{x}-\frac{x}{2} \right )lnx=0\Rightarrow lnx=0\cup \sqrt{x}-\frac{x}{2}=0\]da cui \[lnx=0\Rightarrow x=1\cup \sqrt{x}-\frac{x}{2}=0\Rightarrow x=\frac{x^{2}}{4}\Rightarrow x=4, x =0\] e la soluzione x = 0 non è accettabile.
Si poteva accertare per verifica diretta che x = 1 è soluzione dell’equazione e quindi supponendo x > 0 e diverso da 1 proseguire con le regole delle potenze, ovvero uguagliare gli esponenti ottenendo l’equazione \[\sqrt{x}=\frac{x}{2}\] da cui le soluzioni x = 0 (non accettabile) e x = 4.
Risolvi in R anche \[ x^{x^{4}}=64\]
Esempio 4.- Risolvere la seguene equazione \[ln^{2}x-3lnx+2=0\] \[log_{2}^{2}\, x^{2}+4log_{2}\, \sqrt{x}-2=0\]
Risolviamo la prima equazione. Posto ln x = t si ha l’equazione di secondo grado nell’incognita t: \[t^{2}-3t+2=0\] avente per soluzioni \[t=\frac{3\pm \sqrt{9-8}}{2}=\left\{\begin{matrix} t_{1} &=1 \\ t_{2} &=2 \end{matrix}\right.\]
e quindi, tenuto conto della poszione ln x = t, si hanno le seguenti due equazioni elementari logaritmiche:\[ln\, x = 1\Rightarrow x=e\, \, \cup\, \, ln\, x =2\Rightarrow x=e^{2}\]
Se non sai risolvere la seconda equazione vedi il mio video su Youtube
Esempio 5.- Risolvere la seguente equazione \[log_{4}(x-\pi- 2)=log_{2}\left ( x-\pi \right )\]
Prima di tutto richiediamo le condizioni di esistenza dei logaritmi: \[\left\{\begin{matrix} x-\pi +2 &>0 \\ x-\pi & >0 \end{matrix}\right.\Rightarrow x>\pi\] quindi trasformiamo l’equazione ad una equivalente ma avente le stesse basi applichiamo la regola di trasformazione delle basi. Tenuto conto che\[log_{2}\left ( x-\pi \right )=\frac{log_{4}\left ( x-\pi \right )}{log_{4}\, 2}=2log\left ( x-\pi \right )\] si ha: \[log_{4}\left ( x-\pi+2 \right )=2log_{4}\left ( x-\pi \right )\Rightarrow log_{4}\left ( x-\pi+2 \right )=log_{4}\left ( x-\pi \right )^{2}\Rightarrow \left ( x-\pi +2 \right )=\left ( x-\pi \right )^{2}\Rightarrow x-\pi +2=x^{2}-2x\pi +\pi ^{2}\Rightarrow x^{2}-x(2\pi -1)+\pi^{2}-2+\pi =0\] e risolta quest’ultimo equazione si ha: \[x_{2}=\pi +1,\, \, \, x_{1}=\pi -2\]
Solo la soluzione maggiore è accettabile.
Risolvere anche la seguente equazione \[log_{4}\left ( 4x+3 \right )=log_{2}\left ( x-1 \right )-log_{4}x\]
Non sai risolverla? Allora vedi il mio video su Youtube
Esempio 6.- Risolvere la seguente equazione \[\frac{1}{lnx-1}+\frac{2}{lnx+1}=\frac{3}{ln^{2}x-1}\]
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube!
Esempio 7.- Risolvere la seguente equazione \[\frac{3}{e^{x}-1}-\frac{1}{e^{x}+1}=\frac{2}{e^{2x}-1}\]
Esempio 8.- Risolvere le seguenti equazioni \[log_{2}^{2}(2x\sqrt{x}+2)-log_{2}\left ( 2x\sqrt{x}+2 \right )-2=0\] \[log_{2}\left ( x^{2}+1 \right )=1+\frac{2}{3}log_{2}\, x+log_{8}\, x\]
Risolviamo la seconda equazione. Vedi il mio video su Youtube
Esempio 9.- Risolvere la seguente equazione \[3^{2\sqrt{x+4}}-3^{\sqrt{x+4}}-4=0\]
\[Log\left ( \sqrt{x-2} -\sqrt{x-1}\right )-Log\left ( \sqrt{x-2}+\sqrt{x+2} \right )=Logx-Log2\]
Risolviamo la seconda equazione assegnata. Non sai risolverla? Vedi il mio video su Youtube
Esempio 10- Risolvere le seguenti equazioni \[2^{x}+\left | 2^{2x} -1\right |=3log_{2}8-\frac{3}{2^{x}}-\frac{7}{2}\] \[log_{2}\left | \left | x^{2}-3 \right |-1 \right |=1\]
Risolviamo la seconda equazione sul mio canale Youtube
Esempio 11- Risolvere la seguente equazione\[log^{2}_{3}\left ( sen\, x+8 \right )-log_{3}\left ( sen\, x+8 \right )=2\]
Esempio 12- Risolvere la seguente equazione\[e^{arctanx}+2=e^{1-arctanx}\]
Esempio 13- Risolvere la seguente equazione\[log_{x}\left ( 3x+2 \right )=log_{(x+2)}(27x+10)\]
Esempio 14- Risolvere la seguente equazione\[log_{\left | x^{2}-5x+9 \right |}\left ( x^{2}-5 \right )=log_{3}(x+1)\]
Esempio 15- Risolvere la seguente equazione \[log_{2}^{3}\, x+6log_{2}^{2}\, x-16log_{2}\, x=0\] Video della risoluzione
