Equilibrio tra domanda e offerta

ll mercato è il luogo economico ove si incontra la domanda di beni da parte dei consumatori con l’offerta dei produttori di beni.

Esistono diverse forme di mercato:

1. di concorrenza perfetta: vi operano un elevato numero di imprese, ognuna produce un bene omogeneo, in condizioni di perfetta informazione e di perfetta mobilità dei fattori produttivi nel lungo periodo. 
2. di monopolio: vi opera un solo venditore
3. di concorrenza monopolistica: 
4. di oligopolio: vi operano poche imprese e ognuna detiene un certo potere di tipo monopolista.

La domanda dei consumatori può essere individuale (una per ogni consumatore) o globale; l’offerta può essere individuale o globale. Nel regime di concorrenza perfetta, che risulta essere un modello puramente teorico,  il prezzo di un bene è unico. Nel seguito ci rifacciamo sempre a questa tipologia di mercato, salvo avviso contrario.
​
Prezzo di equilibrio tra domanda e offerta
Il prezzo di equilibrio è il prezzo in corrispondenza del quale la domanda uguaglia l’offerta.
Per determinare il prezzo di equilibrio in un mercato con domanda d(p) e offerta q(p) bisogna risolvere l’equazione 

d(p) = q(p)

e si accettano le soluzioni reali.

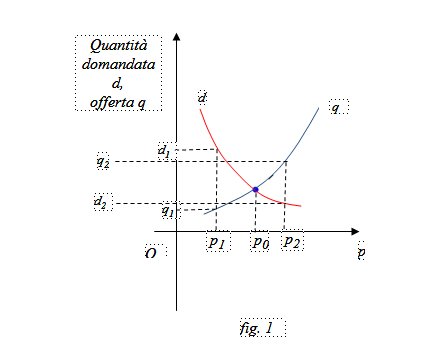
Nella figura 1 si rappresenta sia la curva di domanda d che la curva di offerta q. Al prezzo p1 si ha richiesta di beni pari a d1 e una offerta pari a q1 ; mentre al prezzo al prezzo p2 si ha richiesta di beni pari a d2 e una offerta pari a q2.

Il prezzo p0 è il prezzo di equilibrio, ossia il prezzo in cui la domanda uguaglia l’offerta:

\[al\, \, prezzo\, \, p_{1}\Rightarrow d_{1}>q_{1}\]
(la domanda supera l’offerta di beni)

\[al\, \, prezzo\, \, p_{2}\Rightarrow d_{2}<q_{2}\]
(la domanda è inferiore alla quantità di beni offerti sul mercato)

\[al\, \, prezzo\, \, p_{0}\Rightarrow d=q\]
(la domanda uguaglia l’offerta di beni)
Nelle seguenti figure riportiamo alcuni casi di variazione della domanda e dell’offerta onde mettere in luce come varia il prezzo di un bene al variare della domanda e dell’offerta.

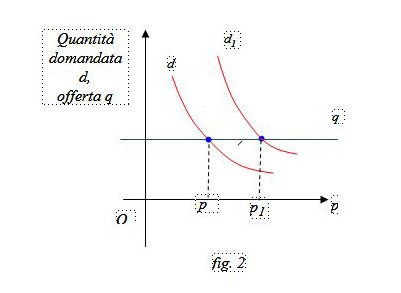
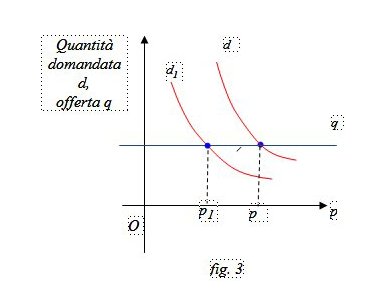
Primo caso. Cambia la domanda d ma l’offerta q resta costante (fig. 2, fig. 3). Nella figura 2 la domanda d aumenta al livello d1 e il prezzo aumenta da p a p1. Nella nella figura 3 invece la domanda d diminuisce al livello d1 e il prezzo diminuisce da p a p1

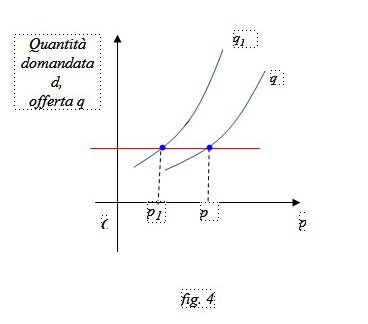
Secondo caso. Cambia l’offerta ma resta costante la domanda (fig. 4, fig. 5)
Nella figura 4 l’offerta aumenta  da q a q1e il prezzo scende da p a p1.

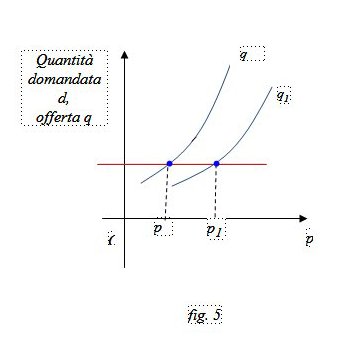
Nella figura 5 l’offerta diminuisce da q a q1 e il prezzo sale da p a p1.

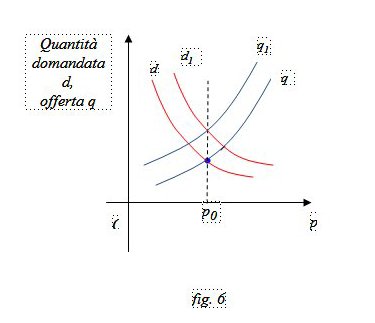
Terzo caso. Cambia l’offerta e la domanda (fig. 6, fig. 7, fig.8)

Nella figura 6 l’offerta aumenta di quanto richiede la domanda e il prezzo resta invariato a p0 .

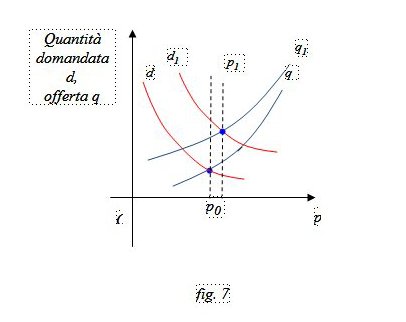
Nella figura 7 l’offerta aumenta meno di quanto richiede la domanda e il prezzo sale da p0 a p1.

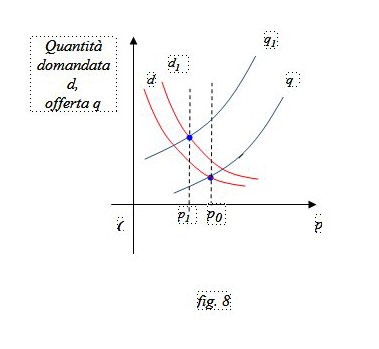
Nella figura 8 l’offerta aumenta più di quanto richiede la domanda e il prezzo scende da p0 a p1.