Esempio 1.1.- Legge di Couloumb.- Due cariche nel vuoto $\displaystyle q=12,5\, \,\mu C$ e $\displaystyle Q=-10\, \,\mu C$ e sono poste a 125 cm di distanza. Calcolare la forza di Coulomb tra le cariche.
Esempio 1.2.- Tre cariche puntiformi sono poste nel vuoto in A, B e C. Sapendo che il segmento AC ha come punto medio il punto B e che le tre cariche valgono $\displaystyle Q_{A}=62,5\, \,nC$, $\displaystyle Q_{B}=20,2\, \,nC$ e $\displaystyle Q_{C}=45,6\, \,nC$ determinare la forza elettrica totale che agisce sulla carica posta in B.
Esempio 1.3.- Tre cariche puntiformi sono poste nel vuoto ai vertici di un triangolo rettangolo ABC retto in B. Sapendo che i cateti AB e BC valgono rispettivamente 35 cm e 55 cm e che le cariche Q_B = 5,0 10^-5 C, Q_A = 4,0 10^-5 C, Q_C = 3,0 10^-5 C, determinare il vettore risultante delle forze agenti su Q_B.
Esempio 2.1.- Campo elettrico di una carica puntiforme e linee del campo elettrico.- Una carica puntiforme q = 5,0 10^-4 C è posta in punto dello spazio in cui è presente un campo elettrico di intensità E = 6,5 10^3 N/C determinare la forza agente sulla carica q.
Esempio 2.2.- Una carica Q genera un campo elettrico E, determinare il valore del campo E a 125 cm da Q.
Esempio 2.3.- Una carica puntiforme Q posta in un punto dello spazio vuoto e una seconda carica q di massa 12 grammi si trova a 3 metri dalla carica Q. Sapendo che la carica q lasciata libera comincia a muoversi con una accelerazione di 4m/s^2 determinare il valore della carica q.
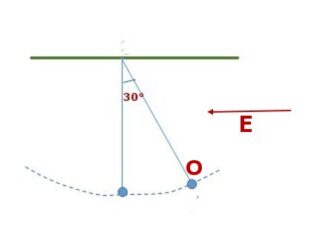
Esempio 2.4.- Una sferetta di massa m e carica q è appesa ad un filo inestendibile ed inclinato di 30° gradi rispetto alla verticale (vedi figura 1), su di essa agisce un campo elettrico E uniforme diretto orizzontalmente e verso sinistra, come indicato nella figura. Sapendo il valore del campo elettrico E e il valore della tensione T nel filo determinare la massa della sferetta e la sua carica elettrica.
Risolvere il problema nel caso particolare T = 4,5 x 10^-2 N e E = 2,5 x 10^5 N/A.
Fig. 1
Risoluzione ragionata
Per calcolare la massa m della sferetta scomponiamo (figura 2) la forza peso in due componenti secondo due direzioni: la prima parallela alla direzione del filo e l’altra ad essa perpendicolare.
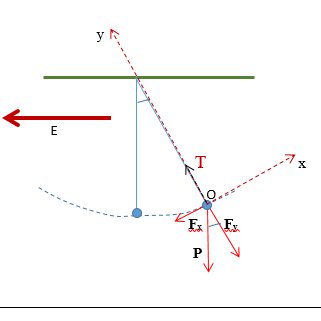Fig. 2
Quindi la forza peso sarà la somma di due forze: $\displaystyle \overrightarrow{P}=\overrightarrow{F_{x}}+\overrightarrow{T}…$ da cui $\displaystyle m\, gcos\, \theta=T \rightarrow m=\frac{T}{g \, cos\, \theta}$, T è la tensione nel filo uguale ae di verso opposto ad $\displaystyle F_{y}$. La sferetta è in equilibrio per l’azione del campo elettrico, se non ci fosse la sferetta si muoverebbe per l’azione della forza $\displaystyle F_{x}$ (vedi pendolo)… dunque il campo elettrico genera una forza uguale e contraria ad $\displaystyle F_{x}$ …
Esempio 2.5.- Una sferetta di massa m e di carica elettrica q è in quiete su di un piano inclinato di 30°, in assenza di attrito. La sferetta è immersa in un campo elettrico uniforme di intensità E e rivolto come in figura. Determinare il valore della carica q.
Risolvere il problema nel caso particolare m = 4,15 x 10^-3 kg e E = 5,45 x 10^4 N/A.
Risoluzione ragionata
Per calcolare la carica q scomponiamo la forza peso, dovuta alla massa della sferetta sul piano inclinato in due componenti secondo due direzioni: la prima parallela alla pendenza del piano inclinato e l’altra perpendicolare al piano inclinato. Cosi facendo la forza peso P sarà la somma di due componenti $\displaystyle \overrightarrow{F_{x}}+\overrightarrow{F_{y}}=\overrightarrow{P}$, con $\displaystyle F_{x}=m\, g\, sen\, \theta$. La sferetta di carica q è tenuta in quiete ( in equilibrio ) dalla forza del campo elettrico, altrimenti tenderebbero a cadere lungo il piano inclinato a causa della forza $\displaystyle F_{x}$ , ovvero agisce una forza dovuta al campo elettrico uguale e contraria ad $\displaystyle F_{x}$ …
Esempio 3.1.- Il flusso del campo elettrico e il teorema di Gauss.- Due cariche puntiformi q_1 e q_2 si trovano nel vuoto a 15 cm di distanza. Quanto vale il campo elettrico nel punto medio tra le posizioni occupate dalle due cariche nell’ipotesi che le cariche q_1 e q_2 siano uguali? E quanto vale il campo E se q_1 = 2q_2?
Esempio 3.2.- In una zona dello spazio vuoto sono presenti 4 cariche elettriche che valgono rispettivamente 1 mC, 2 mC, 3 mC e 4 mC. Se le prime tre cariche sono racchiuse in una superficie S e le ultime due sono racchiuse in una superficie T determinare il flusso del campo elettrico attraverso la superficie S e attraverso la superficie T.
Esempio 4.1.- Campo elettrico di una distribuzione piana infinita di carica e altri campi elettrici con particolari simmetrie.- Determina l’intensità del campo elettrico attraverso un’area di 5.0 cm^2 di un piano infinito uniformemente carico che contiene 12.4 10^-8 C
Esempio 4.2.- Una sfera omogenea di raggio r = 8 cm genera a una distnza di 20 cm dal suo centro un campo elettrico di 2,4 10^ N/C. Determina la carica contenuta nella sfera. Inoltre, nell’ipotesi che la sfera fosse immersa in un mezzo con epsilon_r = 2,6 quale sarebbe la carica contenuta nella sfera?
Esempio 4.3.-
Esempio 5.1.- Energia potenziale elettrica potenziale elettrico e superfici equipotenziali.- Due cariche puntiformi rispettivamente di 2 mC e – 4 mC si trovano ad una distanza di 12, 5 dm nel vuoto. Scegliendo secondo le convenzioni internazionali lo zero calcolare l’energia potenziale del sistema formato dalle due cariche.
Esempio 5.2.- Un oggetto di massa m e di carica q si muove da un punto A ad un punto B nel vuoto per effetto del campo elettrico E. La velocità dell’oggetto nel punto A è VA e nel punto B è VB . Calcolare la differenza di potenziale DV = VB-VA tra i punti A e B.
Risolvere l’esercizio con m = 8,0 x 10^-22 kg, q = 5,5 x10^-16C, VA= 150m/s e VB = 250m/s.
Risolvere l’esercizio con m = 2,0 x 10^-22 kg, q = 1,5 x10^-16C, VA= 200m/s e VB = 350m/s.
Risoluzione ragionata
Esempio 5.3.- Nel vuoto due cariche 2q e -q separate da una distanza d. Calcola il valore del potenziale elettrico nel punto T dell’asse del segmento che congiunge le due cariche situtato ad una altezza h. Calcolare poi il lavoro estero che bisogna compiere per portare una carica Q dall’infinito al punto T senza che la carichi acquisti energia cinetica.
Risolvere il problema nei seguenti due casi particolari:
a) q = 3,5 nC, h = 25 cm; Q 5,3 nC
b) q = -14,6 nC, h = 1,5 m; Q = 22,1 nC
Risoluzione ragionata
Esempio 6.1.- Campo elettrico dedotto dal potenziale
Esempio 7.1.- Circuitazione del campo elettrico
Esempio 8.1.- Capacità di un conduttore e condensatori in serie e parallelo.- Due condensatori, di capacità C_1 e C_2, sono connessi in parallelo e la loro capacità equivalente misura 300 pF. Quando sono posti in serie la loro capacità equivalente è di 50 pF. Quanto valgono le due capacità?
Esempio 8.2.- Due condensatori, di capacità C1 e C2, sono connessi in parallelo e la loro capacità equivalente misura 9 micro F. Quando sono posti in serie la loro capacità equivalente è di 2 micro F. Quanto valgono le due capacità?
Esempio 8.3.- Un condensatore piano è realizzato con due lastre circolari di raggio 11,0 cm poste, in aria, a una distanza di 2,50 mm. Il campo elettrico tra le armature è di 8,02 10^4 V/m. Determinare la capacità del condensatore, la carica di ciascuna armatura e la differenza di potenziale tra le armature
Tratto da “L’ Amaldi per i licei scientifici.blu” – Zanichelli
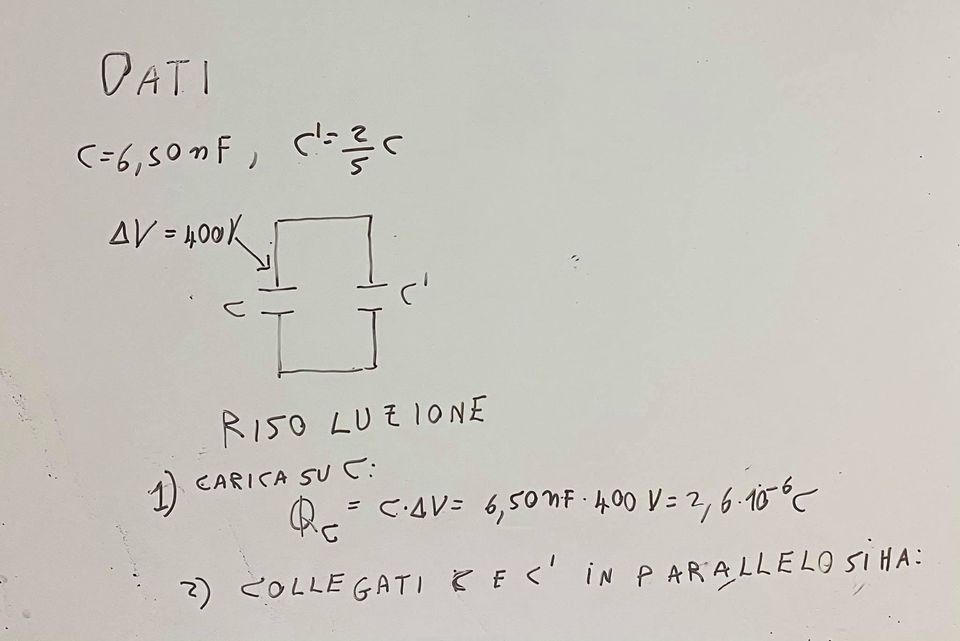
Esempio 8.3.- Un condensatore di capacità C = 6,50 nF è caricato fino ad ottenere una differenza di potenziale fra le sue armature di 400 V. Il condensatore viene staccato dalla sorgente di carica e poi collegato ad un secondo condesatore C’, inizialmente scarico, e tale che C’ = 2/5 C (vedi figura). Determinare la differenza di potenziale ai capi dei due condensatori. Determinare inoltre la carica immagazzinata su ciascun condensatore. [ Tratto da “L’ Amaldi per i licei scientifici.blu” – Zanichelli ]
Risoluzione.
Nelle figure seguenti è indicata la risoluzione dell’esercizio
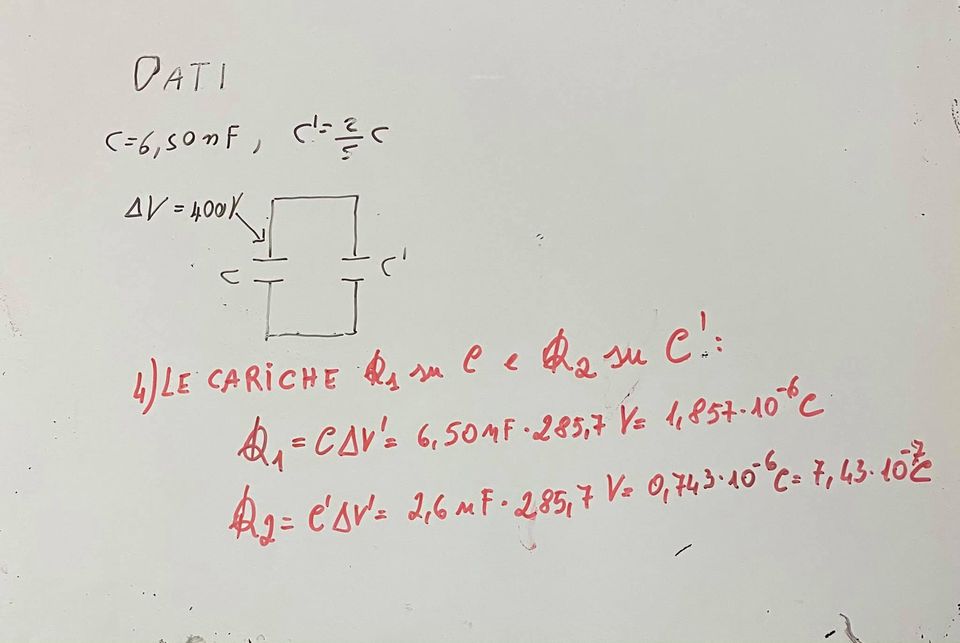
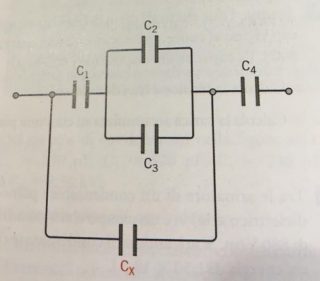
Esempio 8.4.- Determinare la capacità del condensatore $\displaystyle C_{x}$ in modo che il sistema di condensatori piani indicati in figura sia equivalente ad un condensatore di capacità totale \[C_{Tot}=2,40\mu F\] sapendo che \[C_{1}=2,00\mu F,\, C_{2}=1,25\mu F,\, C_{3}=1,75\mu F,\, C_{4}=6,00\mu F\].
[ Tratto da “L’Amaldi per i licei scientifici.blu, Zingarelli Editore. Esercizio N.1 pag. 764 ]
Risoluzione
La capacità equivalente dei condensatori $\displaystyle C_{2}$ e $\displaystyle C_{3}$ , in parallelo, vale \[C_{e}=C_{2}+C_{3}\Rightarrow C_{e}=1,25\mu F+1,75\mu F=3\mu F\]
quella dei condensatori $\displaystyle C_{1}$ e $\displaystyle C_{e}$ in serie vale:
\[\frac{1}{C^{\, ‘}_{e}}=\frac{1}{C_{1}}+\frac{1}{C_{e}}\Rightarrow C^{\, ‘}_{e}=\frac{C_{1}\cdot C_{e}}{C_{1}+C_{e}}\Rightarrow C^{\, ‘}_{e}=\frac{2\cdot 3}{2+3}=\frac{6}{5}\mu F=1,2\mu F\]
Per determinare $\displaystyle C_{x}$ bisogna dunque risolvere il sistema
\[\left\{\begin{matrix} C^{”}_{e}& =C^{‘}_{e}+C_{x}\\ \frac{1}{C_{Tot}} & =\frac{1}{C_{4}}+\frac{1}{C^{”}_{e}} \end{matrix}\right.\]
Si ricava C” e dalla seconda equazione e si sostituisce nella prima e si ha: \[C_{x}=C^{”}_{e}-C^{‘}_{e}=4-1,2=2,80\mu F\]
Esempio 8.5.- Del sistema di condensatori riportati in figura si sa che $\displaystyle C_{1}$ = 350pF, $\displaystyle C_{2}$ = 520 pF, $\displaystyle C_{3}$ = 230 pF e $\displaystyle \Delta V_{AB}=1,50kV$.
Calcolare la capacità equivalente. Determinare inoltre la carica su ciascuna condensatore e la differenza di potenziale ai capi di ognuno di essi.
Tratto da “L’ Amaldi per i licei scientifici.blu” – Zanichelli
Esempio 8.6.- Una particella di carica q e massa m viene lasciata libera da un punto P posto a metà tra le facce di un condensatore piano mantenute a una differenza di pontenziale costante. I valori numerici sono: d = 10cm ; m = 1,0mg; q = 1,0 uC; V=1,0V. A quale distanza in verticale(h) dal punto P deve essere praticato un foro su una faccia del condensatore in modo che la particella carica ci passi attraverso. ( Problema assegnato alle Olimpiadi di Fisica)
Risoluzione
Tra le facce del condensatore il campo elettrico è costante nello spazio e quindi si ha $\displaystyle E=\frac{V}{d}$, mentre sulla carica agiscono la forza peso verso il basso e la forza dovuta al campo elettrico.
Sull’asse delle x la carica avrà accelerazione pari ad $\displaystyle a=\frac{q\cdot V}{m\cdot d}$ e quindi possiamo ricavare il tempo che impiega per raggiungere la faccia del condensatore; nello stesso tempo la carica percorrerà uno spazio in verticale con accelerazione g e quindi si ha:
$\displaystyle h=\frac{m\cdot g\cdot d^{2}}{q\cdot V}\rightarrow h=4,9\, cm$
Esempio 9.1.- La corrente e le leggi di Ohm e resistenze in serie e parallelo.- Due resistori, di resistenza R1 e R2, sono connessi in parallelo e la loro resistenza equivalente misura 70 kΩ. Quando sono posti in serie la loro resistenza equivalente è di 300 kΩ. Quanto valgono le due resistenze?
Suggerimento: Occorre mettere a sistema…
Esempio 9.2.- Una fibra nervosa (assone) può essere considerata, in prima approssimazione, come un lungo cilindro. Se il suo diametro è di 10 micro m e la sua resistività è 1.6 Ω m, quanto vale la resistenza di una fibra lunga 0,55 m?
Esempio 9.3.- Una resistenza da 180 Ω e una da 360 Ω sono collegate in parallelo fra loro e in serie con una terza resistenza da 220 Ω. Qual è la resistenza equivalente del circuito?
Esempio 9.4.- Una batteria con differenza di potenziale $\displaystyle \Delta V=14,0V$ deve essere collegata a tre resitori di resistenze, R, 2R e 3R, con $\displaystyle R=3.0\, \Omega$. I resistori si devono collegare in modo che due siano in parallelo e uno in serie con la coppia di quelli in parallelo. E visto che vi sono modi diversi di fare il collegamento, determinare la configurazione che dà l’intensità di corrente minima nel circuito. Determinare inoltre l’intensità di corrente minima.
Ripetere l’esercizio per $\displaystyle \Delta V=12,0V$ e $\displaystyle R=2.0\, \Omega$.
Risoluzione ragionata
In base al testo si possono avere tre configurazioni con due resistori in paralleo e il terzo in serie con la coppia dei primi due in parallelo. Precisamente si può avere la coppia R, 2R in parallelo in serie con 3R; poi si può avere la coppia R, 3R in parallelo con 2R in serie e infine si può avere la coppia 2R e 3R in parallelo con il resistore di resistenza R in serie. Pertanto bisogna calcolare per ogni configurazione la resistenza totale e di conseguenza calcolare l’intensità di corrente, $\displaystyle I=\frac{\Delta V}{R_{Tot}}$, e scegliere la configurazione con l’intensità minima di corrente.
Ad esempio per la prima configurazione si ha che la resistenza equivalente dei due resistori in parallelo è $\displaystyle R_{e}=\frac{R\cdot 2R}{R+2R}=\frac{2R}{3}$ e di conseguenza la resistenza totale con il terzo resistore in serie è: $\displaystyle R_{Tot}=\frac{2R}{3}+3R=\frac{11}{3}R$. Quindi l’intensità di corrente della prima configurazione è
$\displaystyle I_{1}=\frac{\Delta V}{R_{Tot}}=\frac{\Delta V}{\frac{11R}{3}}=\frac{3\Delta V}{11\cdot R}=…$
e sostituendo i valori numeri assegnati si ottiene $\displaystyle I_{1}=1,3\, A$. Calcolare dunque analogamente $\displaystyle I_{2},\, I_{3}$, ossia le correnti della seconda e terza configurazione dei resistori e scegliere il valore minimo ottenuto.
Nota.- Si potevano calcolare anche direttamente le resistenze totali per ogni configurazione e osservare quale era la resistenza massima, il che avrebbe indicato poi la corrente minima.
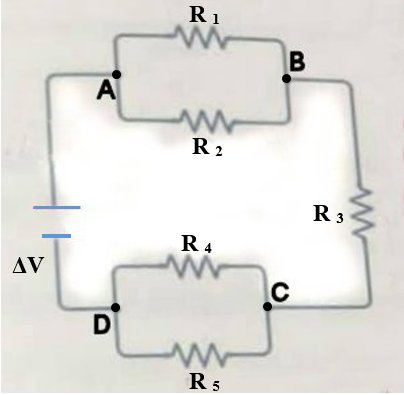
Esempio 10.1.- Circuiti e leggi di Kirchhoff.- Nel seguente circuito, vedi foto, si ha \[\Delta V=48V,\, R_{1}=40\Omega,\, R_{2}=30\Omega ,\, R_{3}=60\Omega ,\, R_{4}=10\Omega ,\, R_{5}=20\Omega.\]
Calcolare la resistenza equivalente del circuito, la corrente totale che circola nel circuito e la corrente che attraversa la resistenza $R_{5}$.
Risoluzione ragionata
Per determinare la resistenza equivalente del circuito calcolare prima la resistanza equivalente delle due coppie di resistenze in parallelo e poi sommare le tre resistenze in serie. Quindi calcolare la corrente I che scorre nel circuito. Per calcolare la corrente che scorre nella resistenza $\displaystyle R_{5}$ calcolare la differenza di potenziale nelle due resistenze $\displaystyle R_{4}$ e $\displaystyle R_{5}$ utilizzare la legge di Ohm $\displaystyle \Delta V_{5}=I\cdot R’_{4,5}$ e quindi calcolare $\displaystyle I_{5}=\frac{\Delta V_{5}}{R_{5}}$
Esempio 10.2.- Nel nodo A del circuito, vedi foto, entra una corrente i = 20,0 A e le tensioni e le resistenze nella figura valgono rispetteivamente… Determinare il verso e il valore delle correnti i1 e i2 che circolano rispettivamente nel ramo LM e nel ramo ON del circuito.
Risoluzione ragionata
Esempio 10.3.- Nel circuito della figura si DV = 12V e R1 =3,0 Ohm, R2 = 4,0 Ohm. Vogliamo che la corrente i2 che attraversa il resistore di resistenza R2 sia inferiore o uguale ad un valore i 2 = 1,5 A. Quale intervallo di valori può assumere Rx?
Risoluzione ragionata
Esempio 10.4.-
NOTA: App utile: Clicca qui https://www.edutecnica.it/apps/kirchoff/kirchoff.htm
Esercizi svolti di elettromagnetismo
Esempio 1.1.- Legge di Ampere
Esempio 2.1.- Valore del campo magnetico
Esempio 3.1.- Filo percorso da corrente
Esempio 4.1.- Spira circolare
Esempio 5.1.- Solenoide e momento magnetico di una spira
Esempio 6.1.- Forza di Lorentz.- Un protone si muove in un campo magnetico uniforme di intensità pari a 2,0 10^-2 tesla, in direzione perpendicolare a quella del campo magnetico. Sapendo che sul protone agisce una forza di modulo pari a 2.0 10^-6 N determinare la velocità del protone.
Esempio 6.2.-Un elettrone si muove in un campo magnetico uniforme di intensità pari a 0,18 T (tesla), in direzione perpendicolare a quella del campo magnetico. Sapendo che sull’elettrone agisce una forza F = 8,9 x 10^-15 N calcolare la velocità dell’elettrone.
Esempio 6.3.-Un elettrone si muove in un campo magnetico uniforme di intensità pari a 0,66 tesla, in direzione perpendicolare a quella del campo magnetico, con una velocità V = 6,27 x 10^5 m/s. Calcolare il raggio R dell’orbita descritta dall’elettrone.
Risoluzione ragionata
Dalla teoria si sa che l’orbita è una circonferenza descritta con moto circolare uniforme. Quindi calcoliamo prima la forza F , poi con il principio fondamentale della dinamica calcoliamo l’accelerazione dell’elettrone e quindi il raggio dell’orbita con la formula R = v^2/a.
Naturalmente bisogna sapere la carica dell’elettrone e la sua massa, ma si possono trovare in rete o sul libro.
R = 5,4 x 10^-6 m
Esempio 6.4.- Ripetere l’esercizio 6.3 sostituendo all’elettrone il protone.
R = 9,9 mm
Esempio 6.5.-
Esempio 7.1.- Flusso del campo magnetico.- Una bobina costituita da 20 spire di raggio 3,0 cm viene immersa in un campo magnetico di intensità pari 0,6 10^-2 Tesla in modo che la superficie delle spire sia perpendicolare alla direzione delle linee del campo. Successivamente la bobina ruota di 90 gradi. Determinare la variazione di flusso del campo magnetico attraverso la bobina.
Esempio 7.2.- Un solenoide lungo 74,35 cm è percorso da una corrente di 4,23 ampere (A) e genera al suo interno un campo magnetico B. Sapendo che ogni spira del solenoide ha area di 25,0 cm^2 e che il flusso del campo magnetico attraverso la superficie trasversale del solenoide stesso è di 11,55 10^-6 Wb (Weber), determinare il numero di spire del solenoide.
Risoluzione ragionata
Prima calcoliamo il campo magnetico con la formula inversa del flusso, poi il numero N di spire del solenoide mediante la formula inversa del campo magnetico.
Esempio 8.1.- Circuitazione del campo magnetico. Un filo rettilineo di lunghezza infinita è percorso da una corrente di 6 10^-1 ampere. Calcolare l’intensità del campo magnetico in un punto P distante 2,5 mm dal filo. Calcolare l’intensità del campo anche a 2 cm dal filo.
Esempio 8.2.- Ai vertici di un triangolo ABC sono collocati tre lunghi conduttori cilindrici paralleli percorsi da correnti elettriche (vedi figura). Sapendo che in C il verso della corrente è entrante nella pagina e in A e B è uscente determinare la circuitazione del campo magnetico lungo il percorso rettangolare di contorno L e lungo la circonferenza circoscritta al triangolo ABC. Si assuma come valori delle correnti valori a piacere.
Esempio 8.3.- Tre fili di lunghezza L = 2,0m e distanti tra loro d = 2,0 cm sono percorsi dalle correnti i1, i2 e i3. I fili sono concatenati al cammino orientato gamma come in figura. Sapendo che la circuitazione del campo magnetico lungo gamma è zero determinare le correnti i1, i2 e i3 sapendo che la forza tra il filo 1 e 2 è di 2,0 N e che quella tra il filo 2 e 3 è di 8 N.
Risoluzione ragionata
Bisogna scrivere un sistema di tre equazioni in tre incognite. Assumiamo come incognite le tre correnti e dal teorema di Gauss per il campo magnetico si ottiene una prima equazione nelle tre incognite, poi mediante le forze tra i fili si ottengono altre due equazioni nelle stesse incognite, da mettere a sistema con la prima…
Esempio 9.1.- Teorema di Ampere
Esempio 10.1.- Legge di Faraday-Neumann e legge di Lenz.-
Esempio 11.1.- Induttanza e coefficiente di autoinduzione e legge di Faraday-Neumann per l’autoinduzione
Esempio 12.1.- Energia e densità di energia del campo magnetico
Esempio 13.1.- Corrente del circuito RL
Esempio 14.1.- Forza elettromotrice alternata, corrente alternata circuiti e trasformatore, impedenza in un circuito RLC in serie. Un’induttanza da 0,38 H e una resistenza da 225 Ohm sono collegate in serie a un generatore di corrente alternata con una tensione efficace di 30 V e una frequenza di 60 Hz. Calcolare i valori efficaci: della corrente nel circuito; della tensione ai capi della resistenza, della tensione ai capi dell’induttanza.
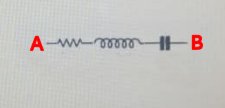
Esempio 14.2.- Gli elementi di un circuito illustrati nella figura sono collegati nei punti A e B a un generatore di corrente alternata. Se la tensione efficace del generatore è 41 V e la sua frequenza è 75 Hz. Sapendo che R = 42 Ohm, L = 150 mH, C = 35 microF qual è la tensione efficace ai capi dell’induttore?
Esempio 15.1.- Un telefonino riceve segnali alla frequenza di 900 mega Hz. Il circuito di ricezione del telefonino ha una induttanza di 3,12 x 10^12 H. Calcolare il valore della capacità contenuta nello stesso circuito di ricezione.
Suggerimento: Applicare la formula \[C=\frac{1}{L\left ( 2\pi f \right )^{2}}\]
Risultato: Circa 1,0 x 10^(-8) F