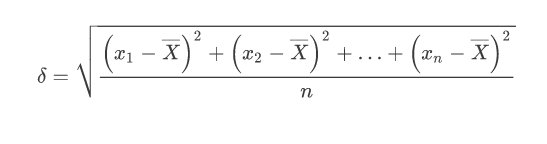- analogici: si legge il valore della msura su di una scala graduata;
- digitali: il risultato della misura è espresso dallo strumento con delle cifre.
Sensibilità portata e prontezza di uno strumento di misura
- La sensibilità è la più piccola variazione della grandezza che lo strumento può misurare.
- La portata è il più grande valore che lo strumento può misurare.
- La prontezza di uno strumento indica la rapidità con cui risponde a una variazione della quantità da misurare.
In ogni misura vi possono essere due tipi di errori:
- Errori sistematici: sono gli errori dovuti ad un difetto dello strumento, a una errata taratura dello strumento, ad una risposta lenta dello strumento nell’atto di misurare, oppure al fatto che lo strumento modifica la grandezza da misurare nell’atto di misurarla.
Questo tipo di errore è sempre dello stipo (sempre per difetto sempre per eccesso) e sono errori prevedibili. Lo sperimentatore deve sempre avere l’obiettivo di eliminarli o di renderli poco influenti, anche se non è sempre tecnicamente facile. - Errori accidentali (o casuali): sono gli errori dovuti a cause accidentali, imprevedibili, a disturbi che influiscono sulla grandezza da misurare, sullo sperimentatore o sullo strumento adoperato per misurare. Questi errori non si possono eliminare.
Dato che tutte le misure sono affette da errori, non ha senso cercare il valore esatto di una grandezza, ma solo quello più probabile. Inoltre, nel comunicare una misura è necessario associarle anche un errore.
Misurazione singola ed errore di lettura.- Se indichiamo con $\displaystyle M_{1}$ il valore di una singola misurazione e con S la sensibilità dello strumento per esprimere la misurazione fatta si scrive:
\[M=M_{1}\pm S\]
Si suole anche dire che il valore della misurazione fatta appartiene all’intervallo di incertezza:
$\displaystyle (M_{1}-S,\, \, \, \, M_{1}+S)$
o anche
$\displaystyle M_{1}-S<M<\, \, M_{1}+S$
Esercizio N. 1.- Se misuriamo un intervallo di tempo con un cronometro al secondo e otteniamo 45 secondi, per indicare la misurazione fatta dell’intervallo temporale dobbiamo scrivere:
( 45 s ± 1 s ) o anche ( 45 ± 1 ) s
il che significa che il valore della misurazione fatta si trova sicuramente nell’intervallo:
44 s < t < 46 s
Se avessimo fatto la stessa misurazione con un cronometro al decimo di secondo (sensibilità 0,1 s) avremmo scritto
45,0 s ± 0,1 s scritto anche ( 45,0 ± 0,1 ) s
il che avrebbe significato che il valore della misurazione si trova tra:
44,9 s < t < 45,1 s
Esercizio N. 2.- Se misuriamo una lunghezza con un metro su cui si leggono i millimetri e se il valore misurato (letto) della lunghezza L in esame è 7,845 metri dobbiamo scrivere:
7,845 m ± 0,001 m scritto anche (7,845 ± 0,001) m
il che significa che il valore della misurazione fatta si trova sicuramente nell’intervallo:
7,844 m < L < 7,846 m
Si può anche scrivere: (7845 ± 1) mm
Serie di misurazioni – Quando si eseguono più misurazioni di una stessa grandezza si ottengono valori differenti dovuti agli errori casuali di misura. Siano allora\[x_{1},x_{2},…,x_{n}\]
i risultati di n misurazioni della stessa grandezza.
In tal caso si sceglie come valore più probabile della misura della grandezza misurata la media aritmetica delle misure fatte e si scrive:
\[\overline{X}\pm \Delta x\]
ove
\[\overline{X}=\frac{x_{1}+x_{2}+x_{3}+…+x_{n}}{n}\]
è la media aritmetica delle misure fatte e rappresenta il valore che meglio approssima il valore vero (non determinabile) della grandezza, ossia è il valore più attendibile; mentre per l’incertezza $\Delta x$ si può assumere la semidispersione assoluta (errore assoluto):
\[\Delta x=\frac{x_{max}-x_{min}}{2}\]
ove $\displaystyle x_{max}$ è il valore più grande delle n misurazioni fatte e $\displaystyle x_{min}$ il valore più piccolo.
Un altro modo di esprimere l’incertezza nel caso di un alto numero di misurazioni eseguite è quello di utilizzare l’errore quadratico medio, o deviazione standard:
ove \[x_{i}-\overline{X},\, \, \, \forall i=1,2,…,n\]
sono gli scarti dalla media. In tal caso scriveremo: \[X=\overline{X}\pm \delta\] e la probabilità che la misura cada nell’intervallo di incertezza è del 68,3%.
Nella formula spesso si trova al denominatore n – 1 invece di n.
Errore relativo:
$\displaystyle E_{r}=\frac{\Delta x}{\overline{X}}$
l’errore relativo non ha unità di misura e indica l’accuratezza della misura: l’errore relativo più è piccolo più è precisa la misurazione fatta.
Errore relativo percentuale:
Errore relativo percentuale = ( errore relativo x 100) %
Accordo entro l’errore e compatibilità di due misurazioni
- Se la previsione teorica per il valore di una grandezza ricade all’interno dell’intervallo definito dall’errore sperimentale, possiamo dire che è in accordo con la misura entro i limiti dell’errore sperimentale
- Date due misurazioni diverse della stessa grandezza ( eseguiamo due esperimenti di misura diversi sulla stessa grandezza), diciamo che le due misure sono compatibili (cioè in accordo entro gli errori) quando entrambi i valori medi ricadono negli intervalli di incertezza delle due misure.
Esercizio N. 3.- Calcolare la misura più probabile l’errore assoluto, l’errore relativo e quello percentuale delle seguenti misure espresse in metri:
2,2 2,3 2,4 2,4 2,5 2,3 2,2 2,6 2,5 2,4.
Come si scrive la misura?
Risoluzione
Si ha:
$\displaystyle \overline{X}=\frac{2,2+2,3+2,4+2,4+2,5+2,3+2,2+2,6+2,5+2,4}{10}=2,38$
valore approssimato a 2,4, mentre l’errore assoluto è: $\displaystyle \Delta x=\frac{2,6-2,2}{2}=0,2$. Si scrive (2,4 ± 0,2) m. Se la sensibilità dello strumento di misura fosse 0,3 m si scriverebbe (2,4 ± 0,3) m, mentre se fosse 0,1 m si scriverebbe (2,4 ± 0,2) m; in pratica si sceglie il valore più grande tra la sensibilità e l’errore assoluto. L’errore relativo è \[E_{r}=\frac{\Delta x}{\overline{X}}=\frac{0,2}{2,4}=0,08 \] e l’errore relativo percentuale è (0,08 x 100) % = 8%.
Esercizio N. 4.- Una bilancia ha una sensibilità di 0,1 kg; si misura due volte un corpo di massa m e si ottengono le seguente 5 misurazioni ogni volta:
Prima misurazione: 3,4 kg, 3,4 kg, 3,4 kg, 3,4 kg, 3,4 kg.
Seconda misurazione: 3,4 kg, 3,4 kg, 3,4 kg, 3,4 kg, 3,5 kg.
Determinare la misura più attendibile, l’errore assoluto, l’errore relativo e l’errore relativo percentuale. Come si scrive la misura? Le due misurazioni sono compatibli?
Risoluzione
Prima misurazione: Media aritmetica 3,4 e misura più attendibile 3,4 kg, Errore assoluto zero, ma si assume la sensibilità (0,1) come errore assoluto perché la sensibilità è più grande dell’errore assoluto calcolato. Errore relativo: $\displaystyle \frac{0,1kg}{3,4kg}=0,029\rightarrow 0,03$, Errore relativo percentuale 3%. La misura si scrive (3,4 ± 0,1) kg
Seconda misurazione: Media aritmetica 3,42, misura più attendibile è 3,4 kg, Errore assoluto $\displaystyle \frac{3,5-3,4}{2}=0,05kg$ ma si assume la sensibilità (0,1) come errore assoluto perché la sensibilità è più grande dell’errore assoluto calcolato. Errore relativo: $\displaystyle \frac{0,1kg}{3,4kg}=0,029\rightarrow 0,03$, Errore relativo percentuale 3%. La misura si scrive (3,4 ± 0,1) kg
Esercizio N. 5.- Con un cronometro si misurano le durate di oscillazioni complete di un pendolo e si ottengono i seguenti valori:
12,6 s, 12,7 s, 12,4 s, 12,6 s, 12,5 s 12,3 s.
Determinare la misura più attendibile, l’errore assoluto, l’errore relativo e l’errore relativo percentuale. Come si scrive la misura?
Risoluzione
Media aritmetica 12,51 e misura più attendibile 12,5 s; Errore assoluto 0,2 s; Errore relativo: $\displaystyle \frac{0,2 s}{12,5 s}=0,016\rightarrow 0,02$, Errore relativo percentuale 2%. La misura si scrive (12,5 ± 0,2) s
Esercizio N. 6.- Misurando sei volte la temperatura corporea di un malato con un termometro digitale si ottengono i seguenti valori:
38,78 °C, 38,81 °C, 38,76 °C, 38,84 °C, 38,835 °C 38,78 °C.
Determinare la misura più attendibile, l’errore assoluto, l’errore relativo e l’errore relativo percentuale. Come si scrive la misura?
Esercizio N. 7.- Misurando sei volte un tratto di una strada per due volte si ottengono i seguenti valori:
Prima volta: 24378 m, 24381 m, 24375 m, 24384 m, 24385 m 24388 m
Seconda volta: 24378 m, 24381 m, 24375 m, 24384 m, 24385 m 24388 m
Determinare la misura più attendibile, l’errore assoluto, l’errore relativo e l’errore relativo percentuale. Come si scrive la misura? Le due misurazioni sono compatibili?
Risultato di una misura con il corretto numero di cifre significative
Per scrivere il risultato di una misura con il corretto numero di cifre significative si usano le regole seguenti:
- L’errore assoluto deve sempre essere arrotondato a una sola cifra significativa;
- L’ultima cifra significativa del risultato di una misura deve essere dello stesso ordine di grandezza dell’errore, cioè nella stessa posizione decimale dell’errore.
Esercizio N. 8.- Un gruppo di persone misura dieci volte l’intervallo di tempo impiegato da un pendolo per compiere una oscillazione completa. Il cronometro utilizzato ha una sensibilità di 0,1 s. Gli studenti ottengono le seguenti misure:
25,8 s, 24,0 s, 21,0 s, 23,2 s, 23,8 s, 23,0 s, 20,2 s, 20,8 s, 23,2 s, 23,8 s.
Calcolare il valore medio e l’errore assoluto. Esprimere la misura ottenuta con il numero corretto di cifre significative.
Risoluzione
Il valore medio è 22,9 s e l’errore assoluto 2,8 s, maggiore della sensibilità. Per rispondere alla seconda domanda arrotondiamo l’errore assoluto ad una cifra significativa e si ha $\displaystyle 2,8\, s\rightarrow 3\, s$, di conseguenza anche il valore medio deve avere l’ultima cifra arrotondata allo stesso ordine di grandezza dell’errore assoluto, e si ha: $\displaystyle 22,9\, s\rightarrow 23\, s$. Quindi il modo corretto di scrivere la misura con il giusto numero di cifre significative è: 23 s ± 3 s.