Esempio 1.1.- Problema del tre composto: 18 cavalli consumano 18 quintali di avena in 20 giorni, in quanti giorni 24 cavalli consumano 12 quintali di avena?
Vedi il mio video se proprio non riesci a risolverlo
Esempio 1.2.- Otto operai lavorando 8 ore al giorno in 15 giorni hanno fatto un muro lungo 60 m, alto 2 metri e largo 0,5 metri. Quanti giorni impiegheranno 30 operai lavorando 6 ore al giorno per fare un muro lungo 80 metri, alto 3 metri e largo 0,60 metri?
Vedi un altro problema del tre composto
Esempio 1.3.- Se una donna in tre giorni fa 6 torte due donne in 4 giorni quante torte fanno?
Vedi come si fa sul mio canale Youtube esempio svolto
Esempio 2.- Problema di ripartizione composta. Si vuole costruire un ponte che si trova alla distanza di 500 metri dal paese P1, a 200 metri dal paese P2, e a 300 metri dal paese P3. I paesi P1, P2, P3 hanno rispettivamente abitanti 1500, 2700 e 3000. Si vuole ripartire la spesa di 5,3 milioni di euro necessaria per costruire il ponte in modo direttamente proporzionale al numero degli abitanti dei tre paesi e in modo inversamente proporzionale alla distanza dei paesi dal ponte. Quanto deve pagare ogni paese?
Non riesci a risolverlo? Vedi il video sul mio canale Youtube
Esempio 3.- Problema di geometria. Determinare la misura di due segmenti sapendo che la somma della loro misura è 52 cm e che il loro rapporto è 4/7
Esempio 4.- Problema di geometria. Determinare la misura di due segmenti sapendo che la somma della loro misura è 56 dm e che il loro rapporto è 3/5
Vedi come risolvere il problema
Esempio 5.- Problema di geometria. Dato un rettangolo di area 1792 dm^2 sapendo che il rapporto delle dimensioni è 4/7 determinare il perimetro del rettangolo.
E vai con il mio video... non è facile da risolvere…
Esempio 6.- Problema di geometria. Dati un rettangolo e un quadrato equivalenti, sapendo che la base AB del rettangolo misura 32 cm e che il perimetro del quadrato misura 64 cm calcolare il perimetro del rettangolo.
Non lo sai risolvere? Allora vedi il mio video su Youtube
Esempio 6.1.-
Esempio 6.2.- Dato un triangolo isoscele di perimetro 320 dm e avente la base uguale ai 6/5 del lato obliquo determinare i lati del triangolo e l’area.
Non lo sai risolvere? Allora vedi il mio video su Youtube
Esempio 7.1- Problemi di geometria. Nella circonferenza di centro O, di raggio AO = 34 cm, tracciamo la corda MN perpendicolare al diametro AB nel punto H e che dista dal centro O di 16 cm, cioè OH = 16 cm.. Vogliamo calcolare l’area della figura AMBN.
Ecco… risolvi…se proprio non riesci prova a vedere il mio video!
Esempio 7.2.1- Problema cerchio e trapezio
Vedi il mio video
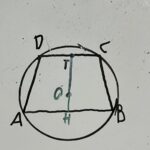
Esempio 7.2.2.- Un trapezio isoscele è inscritto in una circonferenza e le sue basi si trovano da parti opposte rispetto al centro della circonferenza. Sapendo che il raggio della circonferenza è 50 dm e che la base maggiore del trapezio dista 14 dm dal centro della circonferenza e che la base minore misura 60 dm, calcolare la distanza tra le basi, l’area e il perimetro del trapezio.
Risoluzione ragionata
Disegniamo e ragioniamo sulla figura per capire come calcolare la distanza tra le due basi del trapezio.
La distanza tra le due basi del trapezio è il segmento TH, di cui la parte OH è nota. Pertanto per calcolare OT consideriamo il triangolo rettangolo OTC, rettangolo in T e con OC raggio della circonferenza. Di conseguenza possiamo calcolare l’area del trapezio calcolando prima la base maggiore AB = 2xAH, AH si può calcolare ragionando nel triangolo rettangolo AOH rettangolo in H, con AO raggio della circonferenza. Per calcolare il perimetro bisogna calcolare il lato obliquo CB, il che si può fare con il teorema di Pitagora applicato al triangolo CBL, con L proiezione del punto C su AB…
Risultati: Distanza tra le basi: 54 dm; Area 4212 dm^2, perimetro 269,8 dm
Esempio 8.- Area di una figura composta…
Vedi il video con l’esercizio svolto
Esempio 9.- Applicazione del teorema di Pitagora
Vedi il video sul mio canale Youtube
Esempio 10.- Problema di geometria, applicazione dei teoremi di Euclide:
Non lo sai risolvere? Allora vedi il mio video su Youtube
Esempio 10.1.- Vedi un problema svolto
Esempio 11.- Problema di geometria, applicazione dei teoremi di Euclide.
Esempio 12.1.- Geometria solida. Problema sul prisma.- Un prisma retto ha per base un trapezio isoscele. Sapendo che le basi del trapezio misurano rispettivamente 8 cm e 14 cm e che l’altezza del trapezio misura 4 cm determinare l’area totale del prisma e il volume sapendo che l’altezza del prisma misura 7 cm.
Risoluzione
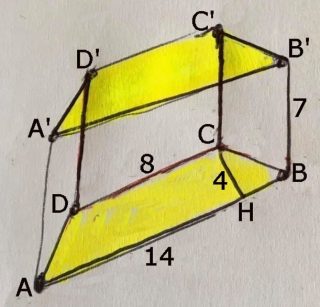
Occorre calcolare il lato obliquo $\overline{CB}$ de trapezio isoscele di base. Pertanto applichiamo il teorema di Pitagora al triangolo rettangolo CHB, ove $\overline{HB}=\left ( \frac{\overline{AB}\, \, \, \, -\, \, \, \, \overline{DC}}{2} \right )$ , e si ha che $\overline{CB}=5\, cm$. Di conseguenza il perimetro del base del prima è P = 32 cm e l’area laterale è $A_{L}=234\, cm^{2}$ . Calcolata l’area di base si ha che l’area totale è 312 cm^2.
Il volume invece è \[V=A_{b}\times h=312cm^{2}\times 7cm=2184cm^{3}\]
Esempio 12.2.- Un prisma retto ha per base un triangolo rettangolo. Sapendo che l’area di base è 600 dm^2 e che un cateto di base è 30 dm determinare l’area totale del prisma sapendo che l’altezza del prisma è 100 dm. Determinare inoltre il volume del prisma e il suo peso ipotizzando che sia fatto di ferro con peso specifico 7,8.
Risoluzione
Calcoliamo prima il secondo cateto del triangolo di base con la formula inversa dell’area, quindi l’ipotenusa del triangolo di base con il teorema di Pitagora. Calcolato il perimetro possiamo calcolare l’area laterale e dunque l’area di base. Il volume si calcola moltiplicando l’area di base per l’altezza e sapendo il peso specifico si può calcolare il peso del prima con la formula $Peso=V\times P_{s}=…$
Esempio 13.1- Problema sulla piramide e peso specifico. Data una piramide quadrangolare regolare di area totale 864 cm^2, sapendo che la sua area laterale è i 4/5 dell’area di base, determinare il volume della piramide.
Provaci … dai… non arrenderti…. Se proprio non riesci vedi il mio video!
Esempio 13.2.- Vedi un altro esercizio svolto
Esempio 13.3,- Un problema sul peso specifico e sulla piramide? Eccolo…. vedi il mio video sul canale Youtube Matematica Facile
Esempio 13.4.- Un altro esercizio sul peso specifico? Eccolo…vedi il video
Esempio 13.5- Una piramide regolare a base un triangolo equilatero e la sua altezza è 40 dm. Sapendo che la sua base è isoperimetrica alla base di un cubo avente volume di 804357 dm^3, calcolare l’area della superficie totale e il volume della piramide. Calcolare inoltre il peso della piramide sapendo che la piramide è d’oro, peso specifico 19,25 kg/dm^3
Esempio 13.6.- Una piramide retta ha per base un rombo con le diagonali aventi per somma 56 dm e per rapporto 3/4. Sapendo che l’apotema è uguale allo spigolo di un cubo avente il volume di 4096 dm^3, calcolare l’area della superficie totale e il volume della piramide.
Per vedere la risoluzione completa degli esercizi 13.5 e 13.6 clicca qui
Esempio 13.7.- Altri problemi sui solidi? Clicca qui
Esempio 14.1.- Problemi con più solidi. Consideriamo tre solidi una piramide quadrangolare regolare d’oro, peso specifico 19,25, un cono circolare retto e una sfera. Si sa che lo spigolo di base della piramide sommato con l’apotema del cono e con il raggio della sfera dà 33 dm e che il raggio della sfera è il doppio dello spigolo di base della piramide, e che l’apotema del cono è i 5/4 del raggio della sfera. Sapendo che l’altezza della piramide è 4 dm e che l’altezza del cono è 12 dm calcolare il peso della piramide e il suo valore economico sapendo che un grammo d’oro vale oggi 44 euro. Calcolare inoltre il volume del cono e il volume della sfera
Non lo sai risolvere? Allora vedi il mio video su Youtube
Esempio 15.- Problema di probabilità classica. Un’urna contiene 5 palline verde, 7 rosse e 8 bianche. Calcolare la probabilità dei seguenti cinque eventi (…vedi video)
Non lo sai risolvere? Allora vedi il mio video su Youtube
Esempio 16.- Geometria analitica.- Dati i punti A, B, C, D del piano cartesiano Oxy determinare area e perimetro del rettangolo ABCD
Esempio 17.- Statistica.- Costruire la tabella delle frequenze per la seguente variabile statistica. Calcolare media aritmetica, mediana e moda, disegnare l’istogramma.