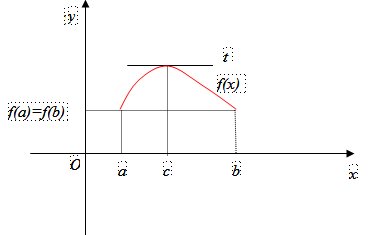Se non ricordi i teoremi puoi ricordali qui
Esempio 1.1.-Teorema di Rolle. Data la funzione $\displaystyle f(x)=\frac{x}{x^{2}+4}$ determinare se esistono i punti che soddisfano al Teorema di Rolle nell’intervallo $\displaystyle \left [ 1,4 \right ]$
Se non sai risolvere l’esercizio puoi vederlo qui
Esempio 1.2.- Data la funzione $\displaystyle f(x)=e^{2x}-3e^{x}+2$ determinare se esistono i punti che soddisfano al Teorema di Rolle nell’intervallo $\displaystyle \left [ 0,ln2 \right ]$
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube
Esempio 1.3.- Data la funzione $\displaystyle f(x)=\frac{x^{2}+1}{2x+1}$, stabilire in quale dei seguenti intervalli soddisfa al teorema di Rolle: $\displaystyle I_{1}=\left [ -1,0 \right ],\, \, I_{2}=\left [ 0,2 \right ],\, \, I_{3}=[0,2[,\, \, I_{4}=\left ( -3,3 \right )$
Esempio 1.4.-Data la funzione \[f(x)=\left | 4-x^{2} \right |\] verificare che essa non soddisfa a tutte le ipotesi del teorema di Rolle nell’intervallo [-3, 3] e che comunque esiste almeno un punto dell’intervallo [-3, 3] in cui si annulla la derivata prima di f(x). Questo esempio contraddice il teorema di Rolle? Motivare la risposta in modo esauriente.
Decimo quesito, Maturità Scientifica 2017.
Esempio 2.1.- Teorema di Lagrange. Data la funzione $\displaystyle f(x)=x^{3}-2x$ determinare se esistono i punti che soddisfano al Teorema di Lagrange nell’intervallo $\displaystyle \left [ -1,3 \right ]$.
Se non lo sai fare vedi il mio video
Esempio 2.2.- Data la funzione $\displaystyle f(x)=log(x^{2})$ determinare se esistono i punti che soddisfano al Teorema di Lagrange nell’intervallo $\displaystyle \left [ -1,2 \right ]$.
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube
Esempio 2.3.- Data la funzione $\displaystyle f(x)=\sqrt{7-x}$ stabilire in quale dei seguenti intervalli verifica il teorema di Lagrange: $\displaystyle \left [ 3,5 \right ],\, \, \left [ 4,7 \right ], \, \, \, \left [ 6,8 \right ]$
Esempio 2.4.- Data la funzione \[f(x)=\left\{\begin{matrix} x^{3} & se\, \, 0\leq x\leq 1\\ x^{2}-kx+k &\, se\, \, 1< x \leq 2 \end{matrix}\right.\]
determinare k in modo che nell’intervallo [0,2] sia applicabile il teorema di Lagrange e trovare il punto di cui la tesi del teorema assicura l’esistenza.
Nono quesito, Maturità Scientifica 2015
Esempio 2.5.- Si mostri che la funzione $\displaystyle y=x^{3}+8$ soddisfa alle condizioni del teorema del valor medio (o teorema di Lagrange) sull’intervallo [-2, 2]. Si determinino i valori medi forniti dal teorema e se ne illustri il significato geometrico.
Quinto quesito, Maturità Scientifica 2007
Esempio 2.6.- Data la funzione \[f(x)=\begin{cases} e^{kx}+p& \text{ se } x>0 \\ px^{3}+k& \text{ se } x\leq 0 \end{cases}\] determinare i parametri reali k e p in modo che tale funzione soddisfi il teorema di Lagrange nell’intervallo [-1, 1] e determinare il punto c definito da tale teorema.
Risoluzione
La funzione f(x) è definita in R e dunque anche nell’intervallo [-1, 1], è continua in quanto i due rami di cui è composta sono continui, continua anche nel punto x = 0, inoltre è derivabile nell’intervallo aperto ]-1, 1[ e la derivata è
$f'(x)=\begin{cases} ke^{kx}& \text{ se } x>0 \\ 3px^{2}& \text{ se } x\leq 0 \end{cases}$
I valori richiesti di k e p sono k = 0, p = -1 e si ottengono mettendo a sistema le seguenti due equazioni in p e k:
\[ \displaystyle \lim_{x \to 0^{+}}e^{kx}+p=f(0)\rightarrow 1+p=k\]
\[\displaystyle \lim_{x \to 0^{+}}ke^{kx}=f'(0)\rightarrow k=0\]
Quindi la funzione richiesta è \[f(x)=\begin{cases} 0& \text{ se } x>0 \\ -x^{3}& \text{ se } x\leq 0 \end{cases}\] e la derivata è
\[ f'(x)=\begin{cases} 0& \text{ se } x>0 \\ -3x^{2}& \text{ se } x\leq 0 \end{cases}\]
Per calcolare il valore di c costruiamo l’equazione del teorema di Lagrange
\[ f'(x)=\frac{f(b)-f(a)}{b-a}\rightarrow f'(x)=\frac{0-1}{2}\]
ed essendo per x >0 la derivata sempre nulla si ha 0 = -1/2 il che è falso e dunque per x > 0 non esiste alcun punto che soddisfa il teorema di Lagrange.
Mentre per x minore o uguale di zero si ha:
\[-3x^{2}=\frac{0-1}{2}\rightarrow 3x^{2}=\frac{1}{2}\rightarrow x=\pm \frac{\sqrt{6}}{6}\]
dunque l’unico valore che soddisfa il teorema di Lagrange è \[c=-\frac{\sqrt{6}}{6}\]
Esempio 3.1.- Teorema di Cauchy. Date le funzioni $\displaystyle f(x)=3x^{2}-1,\, \, g(x)=6x$ stabilire in quale dei seguenti intervalli soddisfano al teorema di Cauchy: $\displaystyle \left [ -2,0 \right ],\, \, \left [ 0,1 \right ],\, \, \left [ 1000,1011 \right ]$
Esempio 3.2.- Teorema di Cauchy. Date le funzioni $f(x)=\frac{x-1}{x+2}$ e $g(x)=\frac{x+1}{x+2}$ stabilire se verificano il teorema di Cauchy nellintervallo [-1, 1].
Applicazioni particolari sui teoremi di Rolle, Lagrange e Cauchy.
Esempio 4.1.- Data la funzione \[f(x)=\left\{\begin{matrix} ax^{2}+x+1 &se\, \, \, -2\leq x\leq 0 \\ b\cdot tanx+c & se\, \, \, \, 0<x\leq \frac{\pi }{4} \end{matrix}\right.\]
calcolare a, b, c in modo che tale funzione soddisfi al teorema di Rolle. Se non sai risolvere l’esercizio vedi il mio video
Esempio 4.2.- Utilizza il teorema di Lagrange per spiegare se è vero che quando un’auto si muove in autostrada senza soste di un tratto AB con velocità media 100 km/h, allora c’è almeno un istante in cui la velocità è uguale a 100km/h.
Esempio 4.3.-** Dimostrare che la funzione \[f(x)=\frac{x+1}{x-1}cos\left ( \frac{2}{x^{2}+1} \right )\] ammette almeno due punti in cui la derivata prima si annulla.