- Le prove assegnate tra il 1928 e il 1969, clicca qui
- Le prove d’esame proposte tra il 1970 e il 2002. Per vedere tutte le prove (risolte) di questo periodo clicca qui
- Mentre per vedere quelle assegnati dal 2001 (Quesiti: clicca qui) fino al 2020 ( Problemi: clicca qui.)
Sessione ordinaria 1970.- Verificare che le due curve piane, grafici cartesiani delle funzioni:
\[y=x^{3}+3x^{2}+3x+1,\, \, \, \, \, y=x^{3}-3x^{2}-3x+1\]
hanno due punti in comune. Indicare l’andamento dei predetti grafici cercandone in particolare gli eventuali punti di massimo o minimo relativo. Determinare l’area della regione piana limitata dai due archi dei grafici aventi per estremi i due punti comuni.
Considerate poi le tangenti ai due grafici nei punti comuni, calcolare l’area del quadrilatero convesso da esse determinato.
Sessione ordinaria 1981.-
1) In un sistema di assi coordinati cartesiani si scrivano le equazioni delle due circonferenze passanti per l’origine O ed aventi i centri rispettivamente nei punti: C'(2,0), C”(-1/2, 0) .
Condotte per il punto O due rette mutuamente perpendicolari, delle quali, la prima incontra le due circonferenze, oltre che nel punto O, nei punti A e B rispettivamente e la seconda nei punti C e D, si determini il quadrilatero ACBD avente area massima.
2) Si studi la funzion $\displaystyle y=x^{2}+\frac{16}{x^{2}}$ e se ne disegni il grafico. Si scrivano le equazioni delle due parabole con gli assi paralleli all’asse delle ordinate, passanti per l’estremo relativo A della curva d’ascissa positiva, per il punto B della curva d’ascissa x =1 e tali che l’area della regione finita di piano limitata dall’arco AB della curva e da ciascuna delle due parabole sia 7/3.
3) In un triangolo di base AB = a e CH = h inscriva il rettangolo con un lato su AB ed i vertici opposti sugli altri due lati, che in una rotazione completa attorno alla retta AB genera il solido di volume massimo.
Supposto che gli angoli adiacenti alla base siano uno doppio dell’altro, si calcolino i valori che essi assumono quando detto valore massimo è $\displaystyle \frac{\pi a^{3}}{36}$
4) Si dimostri l’identità:
\[\binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1}\]
Risoluzione del primo quesito del 1981





Sessione ordinaria 1996.- 1° Quesito.
In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), sono assegnate le parabole di equazione:
\[y=\frac{1}{4}x^{2}+\frac{1}{4}ax-a^{2}\]
dove a è un numero reale positivo.
Tra di esse determinare la parabola p che, con la sua simmetrica q rispetto all’origine O, delimita una regione di area 128/3.
Constatato che per la parabola p risulta a = 2, calcolare l’area del quadrilatero convesso individuato dagli assi di riferimento e dalle tangenti alle due parabole p, q nel loro punto comune di ascissa positiva.
Considerato infine il quadrilatero convesso avente per vertici i punti medi dei lati del quadrilatero precedente, dimostrare che si tratta di un parallelogramma e calcolarne l’area.
Risoluzione del primo quesito
L’equazione della parabola q, simmetrica di p rispetto all’origine O, è:
\[y=-\frac{1}{4}x^{2}+\frac{1}{4}ax+a^{2}\]
il che si vede mutando nell’equazione di p y in – y e x in – x. Risolvendo il sistema il sistema tra le due parabole si ottengono i punti d’intersezione $\displaystyle R\left ( -2a,-\frac{1}{2}a^{2} \right ),\, \, \, \, \, T\left ( 2a,\frac{1}{2}a^{2} \right )$.
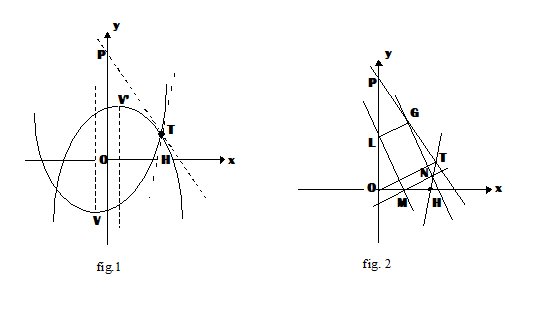
L’area S racchiusa (fig. 1) tra le due parabole è:
$\displaystyle S=\int_{-2a}^{2a}\left ( -\frac{1}{2}x^{2}+2a^{2} \right )dx=\left [-\frac{1}{3}x^{3}+2xa^{2} \right ]_{-2a}^{2a}=\frac{16}{3}a^{3}$
e dalla condizione S = 128/3 si ottiene l’equazione in a:
$\displaystyle 128/3=\frac{16}{3}a^{3}$
ossia a = 2. Di conseguenza le parabole p e q hanno rispettivamente equazioni:
\[y=\frac{1}{4}x^{2}+\frac{1}{2}x-4\]
\[y=-\frac{1}{4}x^{2}+\frac{1}{2}x+4\]
e il punto comune ad esse e di ascissa positiva è: T(4,2).
Sessione ordinaria 2002.- 1° Quesito.
In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), è assegnata la curva k di equazione y = f(x), dove è:
\[f(x)=\frac{x^{2}+2}{x^{3}+2}\]
a) Determinare per quali valori di x essa è situata nel semipiano y > 0 e per quali nel semipiano y < 0.
b) Trovare l’equazione della parabola passante per l’origine O degli assi e avente l’asse di simmetria parallelo all’asse y, sapendo che essa incide ortogonalmente la curva k nel punto di ascissa –1.
(N. B.: si dice che una curva incide ortogonalmente un’altra in un punto se le rette tangenti alle due curve in quel punto sono perpendicolari).
c) Stabilire se la retta tangente alla curva k nel punto di ascissa –1 ha in comune con k altri punti oltre a quello di tangenza.
d) Determinare in quanti punti la curva k ha per tangente una retta parallela all’asse x
e) Enunciare il teorema di Lagrange e dire se sono soddisfatte le condizioni perché esso si possa applicare alla funzione f(x) assegnata, relativamente all’intervallo $\displaystyle -\sqrt{2}\leq x\leq 0$.
Tutte le prove svolte dal 1970 al 2002: clicca qui
