Lo svolgimento di alcuni problemi si può consultare, o si potrà consultare a breve, nel mio canale Youtube
Maturità Scientifica 2021 – Covid 2019/20 clicca qui
Maturità Scientifica 2020 – Covid 2019/20 clicca qui
Maturità Scientifica 2019 – Problema 1. Si considerino le funzioni \[f(x)=ax^{2}-x+b,\, \, g(x)=(ax+b)e^{2x-x^{2}}\]
Provare che, comunque siano scelti a e b in R con a diverso da zero, la funzione g ammette un massimo e un minimo assoluti. Determinare i valori di a e b in corrispondenza dei quali i grafici delle due funzioni f e g si intersecano nel punto A(2,1)
Si assuma d’ora in avanti che a = 1, b = -1. Studiare le due funzioni così ottenute, verificando che il grafico di g ammette un centro di simmetria e che i grafici di f e g sono tangenti nel punto B(0,-1).
Determinare inoltre l’area S della regione piana delimitata dai grafici di f e g.
Si supponga che nel riferimento Oxy le lunghezze siano espresse in metri (m). Si considerino tre fili conduttori rettilinei disposti perpendicolarmente al piano Oxy e passanti rispettivamente per i punti:
\[P_{1}\left ( \frac{3}{2} ,0\right ),P_{2}\left ( \frac{3}{2} ,1\right ),P_{3}\left ( \frac{3}{2} ,-\frac{1}{2}\right )\]
I tre fili sono percorsi da correnti continue di intensità \[i_{1}=2,0\, A,\, i_{2},\, i_{3}\] Il verso di $i_{1}$ è indicato nella figura mentre gli altri due versi non sono indicati. Stabilire come varia la circuitazione del campo magnetico, generato dalle correnti $i_{1},\, i_{2},\, i_{3}$ lungo il contorno di S, a seconda dell’intensità e del verso di $i_{2},\, i_{3}$
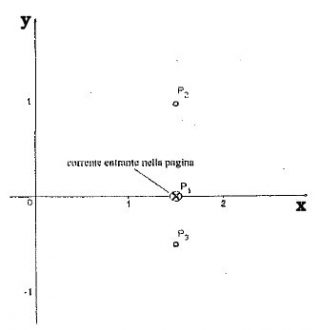
Si supponga, in assenza dei tre fili, che il contorno della regione S rappresenti il profilo di una spira conduttrice di resistenza $R=0,20\Omega$. La spira è posta all’interno di un campo magnetico uniforme di intensità $B=1,5\times 10^{-2}T$ perpendicolare alla regione S. Facendo ruotare la spira intorno all’asse x con velocità angolare w costante, in essa si genera una corrente indotta la cui intensità massima è pari a $5,0\, mA$ . Determinare il valore di w.
Maturità Scientifica 2018 – Problema 2. Consideriamo la funzione \[f_{k}:R\rightarrow R\] così definita:
\[f_{k}(x)=-x^{3}+kx+9\]
con $k\in Z$
1. Detto $\displaystyle \Gamma _{k}$ il grafico della funzione, verifica che per qualsiasi valore del parametro k la retta kr , tangente a $\displaystyle \Gamma _{k}$ nel punto di ascissa 0 e la retta ks , tangente a $\displaystyle \Gamma _{k}$ nel punto di ascissa 1, si incontrano in un punto M di ascissa x =2/3
2. Dopo aver verificato che k = 1 è il massimo intero positivo per cui l’ordinata del punto M è minore di 10, studia l’andamento della funzione $f_{1}(x)$ determinandone i punti stazionari e di flesso e tracciandone il grafico.
3. Detto T il triangolo delimitato dalle rette $r_{1},\, \, s_{1}$ e dall’asse delle ascisse, determina la probabilità che, preso a caso un punto $P\left ( x_{P},y_{P} \right )$ all’interno di T, questo si trovi al di sopra di $\displaystyle \Gamma _{1}$ (cioè che si abbia $y_{P}>f_{1}\left ( x \right )$ per tale punto P).
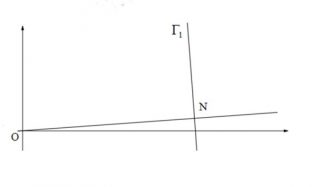
4. Nella figura è evidenziato un punto $N\in \Gamma _{1}$ e un tratto del grafico $\displaystyle \Gamma _{1}$ La retta normale a $\displaystyle \Gamma _{1}$ in N (vale a dire la perpendicolare alla retta tangente a $\displaystyle \Gamma _{1}$ in quel punto) passa per l’origine degli assi O. Il grafico $\displaystyle \Gamma _{1}$ possiede tre punti con questa proprietà. Dimostra, più in generale, che il grafico di un qualsiasi polinomio di grado n > 0 non può possedere più di 2n – 1 punti nei quali la retta
normale al grafico passa per l’origine.
Risoluzione
I punti 1 e 2. Le tangenti alla curva nei punti di ascissa x = 0 e x = 1 sono rispettivamente:
\[y-f(0)=f'(0)(x-0)\Rightarrow\]
\[\Rightarrow y-9=kx\Rightarrow\]
\[\Rightarrow y-9=kx\Rightarrow y=kx+9\]
e
\[y-f(1)=f'(1)(x-1)\Rightarrow\]
\[\Rightarrow y-k-8=(-3+k)(x-1)\]
\[\Rightarrow y=(-3+k)x+11\]
mettendo a sistema le due rette si ha: \[\left\{\begin{matrix} y=(-3+k)x+11 & \\ y=kx+9 & \end{matrix}\right.\] e risolto il sistema si vede che la soluzione del sistema è indipendente da k ed x = 2/3. L’ordinata del punto M, ottenuta sostituendo x = 2/3, in una delle due rette è: \[y=\frac{2k}{3}+9\] ed è minore di 10 se:
\[\frac{2k}{3}+9<10\Rightarrow 2k+27<30\Rightarrow \]
\[\Rightarrow 2k<3\Rightarrow k<\frac{3}{2}\]
Ed è vero che k = 1 è il massimo intero positivo per il quale l’ordinata di M è minore di 10, infatti +1 è il più grande intero positivo appartenente all’insieme definito dalla condizione k < 3/2.
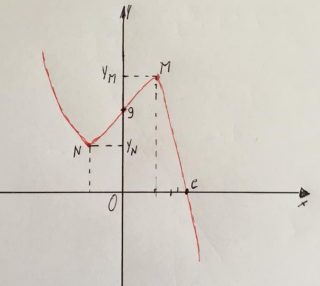
La funzione \[y=-x^{3}+x+9\] ha per dominio R ed è continua, non ammette asintoti essendo razionale intera, e però tende a meno infinito per x che tende a più infinito e a più infinito per x che tende a meno infinito. La positività non si può risolvere elementarmente, ma con metodo grafico si può stabilire che la funzione è positiva per x < c, nulla in x = c e negativa per x > c, ove c è un valore positivo ( si può dimostrare che c è compreso tra 2 e 3).
L’analisi della derivata prima ci permette di stabilire che la funzione ammette un minimo relativo N e un massimo relativo M:
\[y’=-3x^{2}+1\Rightarrow y’\geq 0\Rightarrow\]
\[\Rightarrow -\frac{\sqrt{3}}{3}\leq x\leq \frac{\sqrt{3}}{3}\]
\[N\left ( -\frac{\sqrt{3}}{3},y_{N} \right ),\, \, M\left ( \frac{\sqrt{3}}{3},y_{M} \right )\]
\[con\, \, \, y_{N}<y_{M}\]
L’analisi della derivata seconda ci permette di stabilire che la funzione presenta un flesso in x = 0 di ordinata y = 9. Dai dati acquisiti si può disegnare il grafico della funzione.
Maturità Scientifica 2017 – Problema 2. Consideriamo la funzione f : ℝ → ℝ, periodica di periodo T = 4 il cui grafico, nell’intervallo [0; 4], è il seguente:
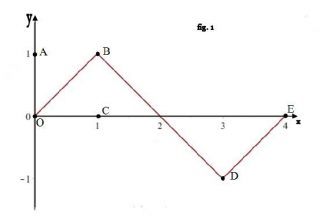
Come si evince dalla figura 1, i tratti OB, BD, DE del grafico sono segmenti i cui estremi hanno coordinate: (0, 0), (1, 1), (3, −1), (4, 0).
1) Stabilisci in quali punti del suo insieme di definizione la funzione f è continua e in quali è derivabile e verifica l’esistenza dei limiti: \[\lim_{x\rightarrow +\infty }f(x),\, \, \lim_{x\rightarrow +\infty }\frac{f(x)}{x}\]; qualora esistano, determinane il valore. Rappresenta inoltre, per x ∈ [0; 4], i grafici delle funzioni:\[g(x)=f'(x),\, \, \, \, \, h(x)=\int_{0}^{x}f(t)dt\]
2) Considera la funzione:\[s(x)=sen(bx)\] con b costante reale positiva; determina b in modo che s(x) abbia lo stesso periodo di f(x). Dimostra che la porzione quadrata di piano OABC in figura 1 viene suddivisa dai grafici di f(x) e s(x) in 3 parti distinte e determina le probabilità che un punto preso a caso all’interno del quadrato OABC ricada in ciascuna delle 3 parti individuate.
3) Considerando ora le funzioni:\[f(x)^{2}\, \, e\, \, s(x)^{2}\] discuti, anche con argomentazioni qualitative, le variazioni (in aumento o in diminuzione) dei 3 valori di probabilità determinati al punto precedente.
4) Determina infine il volume del solido generato dalla rotazione attorno all’asse y della porzione di piano compresa tra il grafico della funzione ℎ per x ∈ [0; 3] e l’asse delle x.
Maturità Scientifica 2016 – Problema 2. Nella figura 1 è rappresentato il grafico Γ della funzione continua f : [0, +∞) → ℝ, derivabile in ]0, +∞), e sono indicate le coordinate di alcuni suoi punti.
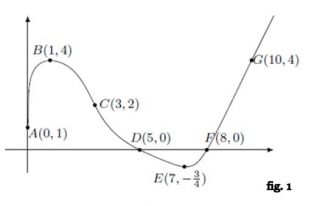È noto che Γ è tangente all’asse y in A, che B ed E sono un punto di massimo e uno di minimo, che C è un punto di flesso con tangente di equazione 2x + y − 8 = 0. Nel punto D la retta tangente ha equazione x + 2y − 5 = 0 e per x ≥ 8 il grafico consiste in una semiretta passante per il punto G. Si sa inoltre che l’area della regione delimitata dall’arco ABCD, dall’asse e dall’asse y vale 11, mentre l’area della regione delimitata dall’arco DEF e dall’asse x vale 1.
1. In base alle informazioni disponibili, rappresenta indicativamente i grafici delle funzioni
\[y=f'(x)\] \[F(x)=\int_{0}^{x}f(t)dt\]
Quali sono i valori di f′(3) e f′(5)? Motiva la tua risposta. [ Non sai risolvere questa prima parte? Vedi il mio video sul mio canale Youtube ]
2. Rappresenta, indicativamente, i grafici delle seguenti funzioni: \[y=\left | f'(x) \right |,\, \, y=\left | f(x) \right |’,\, \, y=\frac{1}{f(x)}\] specificando l’insieme di definizione di ciascuna di esse.
3. Determina i valori medi di y = f(x) e di y = |f(x)| nell’intervallo [0, 8], il valore medio di
y = f ′(x) nell’intervallo [1, 7] e il valore medio di y = F(x) nell’intervallo [9,10].
4. Scrivi le equazioni delle rette tangenti al grafico della funzione F(x) nei suoi punti di ascisse 0
e 8, motivando le risposte.
Maturità Scientifica 2015 – Problema 2. La funzione derivabile y = f(x) ha, per ∈ [−3, 3], il grafico Γ, disegnato in figura 2. Γ presenta tangenti orizzontali per x = −1, x = 1, x = 2. Le aree delle regioni A, B, C e D sono rispettivamente 2, 3, 3 e 1. Sia g(x) una primitiva di f(x) tale che g(3) = −5.
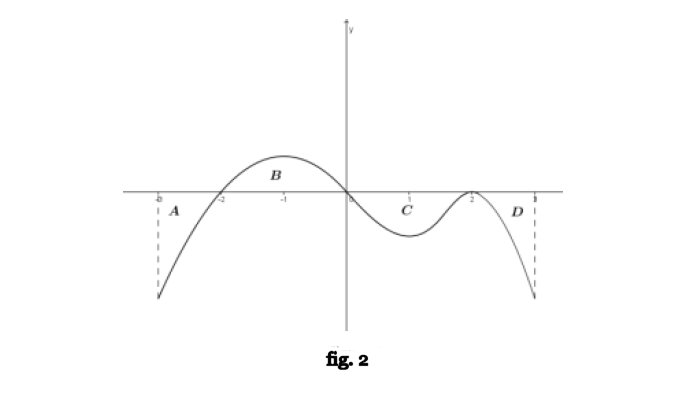1. Nel caso f(x) fosse esprimibile con un polinomio, quale potrebbe essere il suo grado minimo?
Illustra il ragionamento seguito.
2. Individua i valori di x∈ [−3, 3], per cui g(x) ha un massimo relativo e determina i valori di x per i quali g(x) volge la concavità verso l’alto.
3. Calcola g(0) e, se esiste, il \[\lim_{x\rightarrow 0}\frac{1+g(x)}{2x}\]
4. Sia ℎ(x) = 3 ∙ f(2x + 1), determina il valore di \[\int_{-1}^{2}h(x)dx\]
Maturità Scientifica 2014 – Problema 2. A lato (sotto) è disegnato il grafico $\displaystyle \Gamma$ della funzione \[f(x)=x\sqrt{4-x^{2}}\]
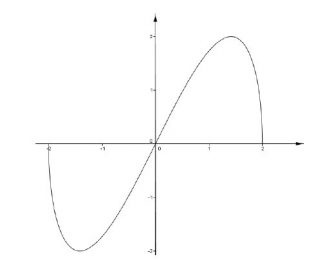
1. Si calcolino il massimo e il minimo assoluti di f(x)
2. Si dica se l’origine O è centro di simmetria per $\displaystyle \Gamma$ e si calcoli, in gradi e primi sessagesimali, l’angolo che la tangente in O a $\displaystyle \Gamma$ forma con la direzione positiva dell’asse x .
3. Si disegni la curva d’equazione \[y^{2}=x^{2}\left ( 4-x^{2} \right )\] e si calcoli l’area della parte di piano da essa racchiusa.
4. Sia \[h(x)=senf(x)\] con \[0\leq x\leq 2\]
Quanti sono i punti del grafico di h(x) di ordinata 1? Il grafico di h(x) presenta punti di minimo, assoluti o relativi? Per quali valori reali di k l’equazione h(x) = k ha 4 soluzioni distinte?