Nel seguito riportiamo tre temi assegnati:
TEMA 1 – Liceo Scientifico
Il flusso di un campo magnetico attraverso una spira presenta la seguente espressione \[\left ( 1 \right )\, \, \, \, \varphi _{\vec{B}}\left ( t \right )=\left ( \frac{1}{2}t^{2}-\frac{1}{6}t \right )Wb\]
- Si illustri il procedimento per calcolare l’espressione della forza elettromotrice indotta in funzione del tempo e, successivamente, se ne calcoli il valore nell’istante iniziale t = 0 s analizzando il risultato dal punto di vista fisico. Si rappresenti graficamente la funzione (1) in un sistema di riferimento flusso-tempo.
- Si individui a piacere una funzione, motivando opportunamente la scelta personale operata, che soddisfi le seguenti condizioni:
a) la funzione scelta passi per l’origine O di un sistema di riferimento cartesiano monometrico ortogonale xOy e per il punto A(3, 4);
b) la funzione presenti un massimo assoluto per 0 < x < 3. Si studi la funzione individuata e se ne disegni il grafico. - Si calcoli l’area compresa tra la funzione scelta nel punto 2 e la funzione (1), dopo averle disegnate nello stesso piano di riferimento xOy. Per la presentazione della regione di piano individuata, si può ricorrere al calcolatore grafico utilizzato durante l’anno scolastico 32019/2020.
- Si analizzi la legge fisica che lega la forza elettromotrice indotta alla variazione di flusso del campo magnetico e si fornisca una dimostrazione della stessa ch e evidenzi il più possibile, in maniera personalizzata, il ragionamento condotto, la scelta oculata di leggi e regole, nonché gli aspetti grafici a supporto dell’analisi condotta.
Vedi il video sul mio canale Youtube
OSSERVAZIONE 1.- Dimostrazione grafica del fatto che la parabola richiesta (punto 2) debba avere l’ascissa del vertice compresa tra 3/2 e 3, $\displaystyle \frac{3}{2}<x_{v}<3$ . La dimostrazione si basa sulle proprietà dell’asse di simmetria di una parabola (vedi il video e poi consulta la dimostrazione qui riportata).

- Nella figura 1 è riportato il caso di una parabola che abbia asse di simmetria x = 1, dunque con il massimo assoluto su tale asse, in tal caso la parabola non può passare per O e A perché per simmetria rispetto dovrebbe passare anche per il punto (2,0), simmetrico dell’origine O rispetto all’asse. Dunque in questo caso la parabola non puà avere un massimo assoluto per x compreso tra 0 e 3, ma tutto al più un minimo assoluto (parabola $\displaystyle \gamma _{1}$ ). La parabola $\displaystyle \gamma _{2}$ ha un vertice, massimo assoluto, tra 0 e 3 ma non può passare per A dovendo passare per il punto (2,0)
- Nella figura 2 è riportato il caso di una parabola con asse di simmetria $\displaystyle x=\frac{3}{2}$ , ma in tal caso non esiste poi nessuna parabola passante per O e per A contemporaneamente. La parabola $\displaystyle \gamma _{3}$ ) passa per O ma non per A, in quanto dovendo passare per simmetria per il punto (3,0) non può passare anche per il punto (3,4); la parabola $\displaystyle \gamma _{4}$ ) passa per O e A ma ha un minimo assoluto tra 0 e 3 e non un massimo assoluto; la parabola $\displaystyle \gamma _{5}$ ) passa per A ma non può passare per l’origine O in quanto passa per simmetria per il punto (0, 4), la parabola non può avere due punti distinti con la stessa ascissa.
- Nel caso di figura 3, cioè nel caso in cui la parabola avesse per asse di simmetria la retta x = 2 allora esiste una parabola passante per O e A e con massimo assoluto tra 0 e 3. E’ dunque questa la circostanza che bisogna considerare per poter ricavare la parabola richiesta dal problema, cioè il massimo assoluto, vertice della parabola, deve avere ascissa compresa tra 3/2 e 3, $\displaystyle \frac{3}{2}<x_{v}<3$. Sotto questa condizione è lecito scegliere come ascissa del vertice della parabola $\displaystyle x_{v}=2\Rightarrow -\frac{b}{2a}=2$, o qualsiasi altro valore x compreso $\displaystyle \frac{3}{2}<x_{v}<3$. Con tale scelta si può poi determinare la parabola d’equazione $\displaystyle y=-\frac{4}{3}x^{2}+\frac{16}{3}x$ , che soddisfa al problema.
- Nel caso di figura 4 abbiamo indicato due parabole passanti per O e A ma la prima con vertice di ascissa maggiore di 3 e la seconda con vertice di ascissa minore di zero, dunque escluse. Inoltre la retta OA, cioè la parabola degnere, è esclusa perchè avrebbe come massimo il punto di ascissa x = 3, contro a quanto richiesto dal problema $\displaystyle \frac{3}{2}<x_{v}<3$.
OSSERVAZIONE 2.- Un altro modo di dimostrare che l’ascissa del vertice della parabola deve essere $\displaystyle \frac{3}{2}<x_{v}<3$ affinché il vertice della parabola sia un massimo assoluto è quello di considerare la derivata prima della parabola $\displaystyle y=ax^{2}+bx+c$ e imporla uguale a zero. Infatti la derivata prima della parabola è $\displaystyle y’=2ax+b$ e richiedendo che si annulli si ha
\[y’=0\Rightarrow 2ax+b=0\]
Quindi, tenuto che $\displaystyle b=\frac{4-9a}{3}$, esprimendo a in funzione di x si ha:
$\displaystyle 2ax+\frac{4-9a}{3}=0\Rightarrow 6ax+4-9a=0$
ossia
$\displaystyle a(6x-9)=-4\Rightarrow a=\frac{-4}{6x-9}$
e dovendo essere a negativo segue che deve essere \[6x-9>0\Rightarrow x>\frac{3}{2}\].
Pertanto l’ascissa del vertice deve essere $\displaystyle \frac{3}{2}<x_{v}<3$ ed è lecito scegliere $\displaystyle x_{v}=2$ come ascissa del vertice, ossia del punto di massimo assoluto, e si ha:
\[a=\frac{-4}{6\cdot (2)-9}=-\frac{4}{3}\]
e di conseguenza
\[b=\frac{4-9a}{3}\Rightarrow b=\frac{4-9\left ( \frac{-4}{3} \right )}{3}=\frac{16}{3}\]
In definitiva la parabola scelta ha equazione \[y=-\frac{4}{3}x^{2}+\frac{16}{3}x\]
OSSERVAZIONE 3.- Si può dimostrare che un’altra funzione che soddisfa alle condizioni del punto 2 è $\displaystyle y=-\frac{4}{9}x^{4}+\frac{16}{27}x^{3}+\frac{16}{9}x^{2}$ avente il massimo assoluto in $\displaystyle \left ( 2,\frac{128}{27} \right )$ un minimo relativo in O(0,0) e un massimo relativo in (-1, 20/27).

TEMA 2 – Liceo Scientifico
- Tracciare il grafico $\displaystyle \gamma$ della funzione \[f(x)=\frac{\sqrt{x}}{1+x}\]
a) la funzione f(x) verifica nell’intervallo $\displaystyle \left [ \frac{1}{4},\, \, 4 \right ]$ le ipotesi del teorema di Rolle?
b) determinare l’area A(k) della regione piana limitata da $\displaystyle \gamma$, dall’asse x e dalla retta x = k con k >0
c) determinare il limite: $\displaystyle l=\lim_{k\rightarrow +\infty }\frac{A(k)}{A_{1}(k)}$, essendo $\displaystyle A_{1}(k)$ l’area del triangolo che ha per vertici l’origine O e i punti d’intersezione della retta x = k con l’asse x e la curva - Un semplice circuito in serie è composto da una resistenza di $\displaystyle 150\Omega$, una batteria di 25 V, un interruttore e un condensatore a facce piane parallele (inizialmente scarico) le cui armature hanno un’area $\displaystyle A=1,41\cdot 10^{-3}m^{2}$ e sono poste a una distanza di 5,0 mm l’una dall’altra. L’interruttore è chiuso all’istante t = 0 s.
a) determinare il valore massimo del flusso del campo elettrico e il valore massimo della corrente di spostamento attraverso il condensatore, dopo la chiusura del circuito.
b) Calcola il flusso del campo elettrico e la corrente di spostamento all’istante t = 0,50 ns.
TEMA 3
Il grafico in figura rappresenta l’andamento della funzione $\displaystyle f(x)=\frac{8}{x^{2}+4}$
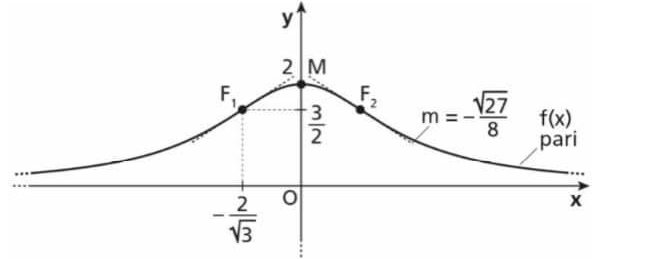
a) Disegna l’andamento probabile del grafico di f ‘(x), senza eseguire lo studio della funzione. Basati sui dati deducibili dal grafico e motiva le scelte effettuate
b) Dimostra mediante la definizione di derivata che la derivata di una funzione derivabile e pari è dispari.
c) Un condensatore piano ha le armature di forma circolare e di raggio R. Supponi di poter trascurare gli effetti al borgo (vedi figura). Spiega l’ipotesi di Maxwell delle correnti di spostamento.
d) Determina l’espressione del campo magnetico indotto B(t) a distanza r < R dall’asse del condensatore se l’intensità del campo elettrico tra le armature varia secondo la legge $\displaystyle E(t)=E_{0}\cdot f\left ( t \right )$ , con $\displaystyle f(t)=\frac{8}{t^{2}+4}$.
Vuoi prepararti per la Maturità Scientifica? Comincia da qui
TEMA 4 – Liceo Scientifico
MATEMATICA.- Studiare la funzione \[f(x)=\frac{x^{2}-x}{x^{2}+1}\]
Sia C la curva rappresentativa di tale funzione. Calcolare l’area della regione finita di piano limitata dalla curva C, dalla retta x = 1 e dall’asintoto orizzontale.
FISICA.- Un condensatore è un sistema elettrico costruito in modo tale da avere una grande capacità. Più condensatori possono essere collegati fra loro per aumentare o diminuire la capacità complessiva disponibile.
Il candidato/a
- Definisca la grandezza fisica “capacità elettrica” di un conduttore, la sua unità di misura nel sistema S.I. e si suoi sottomultipli;
- Descriva la struttura di un condensatore piano spiegando perché essa permette d’aumentare, per quanto possibile, la capacità elettrica del sistema;
- Ricavi e commenti la formula per calcolare la capacità elettrica di un condensatore piano;
- Disegni i simboli grafici di tre condensatori di $\displaystyle 100\mu F$ collegati in modo da ottenere le capacità complessive di $\displaystyle 150\mu F$ e $\displaystyle 300\mu F$ .
Il candidato/a risolva, infine, il seguente problema.
Un sistema di condensatori avente la capacit`a complessiva di 1 mF, a cui `e applicata la d.d.p. di 10 kV, `e fatto scaricare su un resistore con $\displaystyle R=100\Omega$ immerso in un litro d’acqua distillata alla temperatura di 20° C e contenuta in un recipiente isolato termicamente.Il candidato calcoli la temperatura finale dell’acqua dopo che il sistema di condensatori si `e completamente scaricato e spieghi che cosa succederebbe se si fosse raddoppiato il valore della resistenza.
Vuoi lo svolgimento di questo Tema? Clicca qui: Svolgimento Tema 4
