( fig. 1),
sulla quale è fissato come verso positivo il verso antiorario e l’origine degli archi nel punto A(1;0).
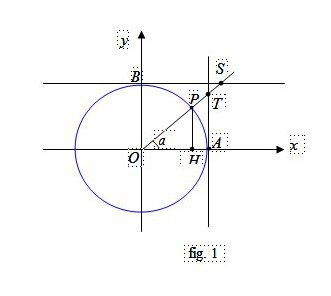
Nella figura 1 si ha:
- seno dell’angolo $\displaystyle \alpha$ è l’ordinata del punto P,
- coseno dell’angolo $\displaystyle \alpha$ è l’ascissa di P,
- la tangente dell’angolo $\displaystyle \alpha$ è l’ordinata di T, la tangente si può indicare anche con tg
- la cotangente dell’angolo $\displaystyle \alpha$ è l’ascissa di S, la cotangente si può indicare anche con ctg o cotg.
Nella figura 1 notiamo che la retta tangente (geometrica) alla circonferenza nel punto A ha equazione x = 1, mentre quella tangente alla circonferenza in B ha equazione y = 1.
Ricordiamo che:
- – 1 è il valore minimo per il seno e il coseno, e si ha: \[-1=sen\left ( \frac{3}{2}\pi \right ),\, \, -1=cos\pi\]
- + 1 è il valore massimo per il seno e il coseno, e si ha: \[+1=sen\left ( \frac{\pi }{2} \right ),\, \, +1=cos\, 0\]
Pertanto le funzioni seno e coseno sono limitate nell’intervallo [ -1, 1 ], il che significa che solo scegliendo un numero y appartenente a [ -1, 1 ] esiste un numero (angolo) reale x tale che sen x = y; analogamente per il coseno.
Mentre se si sceglie un numero y esterno a tale intervallo non esiste un angolo x che abbia y come seno. La tangente e la cotangente invece sono illimitate ovvero qualunque numero reale y si sceglie esiste un angolo x tale che tan x = y (ctg x = y).
Periodicità.- Le funzioni seno e coseno sono periodiche di periodo $\displaystyle P=360^{\circ},\left ( 2\pi \right )$
mentre le funzioni tangente e cotangente di periodo $\displaystyle P=180^{\circ},\left ( \pi \right )$
ossia:
\[sen\left ( \alpha +k360^{\circ} \right )=sen\alpha,\, \, \, cos\left ( \alpha +k360^{\circ} \right )=cos\alpha\]
\[tan\left ( \alpha +k180^{\circ} \right )=tan\alpha,\, \, \, cot\left ( \alpha +k180^{\circ} \right )=cot\alpha\]
con k intero.
Positività delle funzioni goniometriche.- Il seno è positivo nel I e II quadrante, il coseno invece nel I e IV quadrante; il seno è negativo nel III e IV quadrante, mentre il coseno è negativo nel II e III quadrante. La tangente e la cotangente sono positive nel I e III quadrante e negative nel I e IV.
Inoltre si ha:
$\displaystyle sen\alpha >0\, \, \, \Leftrightarrow\, \, 0<\alpha<180^{\circ}$
$\displaystyle sen\alpha <0\, \, \, \Leftrightarrow\, \, 180^{\circ}<\alpha <360^{\circ}$
$\displaystyle cos\alpha >0\, \, \, \Leftrightarrow\, \, 0^{\circ}<\alpha <90^{\circ}\cup 270^{\circ}<\alpha <360^{\circ}$
$\displaystyle cos\alpha <0\, \, \, \Leftrightarrow\, \, 90^{\circ}<\alpha <270^{\circ}$
$\displaystyle tan\alpha >0\, \, \, \Leftrightarrow\, \, 0^{\circ}<\alpha <90^{\circ}\cup 180^{\circ}<\alpha <270^{\circ}$
$\displaystyle tan\alpha <0\, \, \, \Leftrightarrow\, \, 90^{\circ}<\alpha <180^{\circ}\cup 270^{\circ}<\alpha <360^{\circ}$
$\displaystyle cot\alpha >0\, \, \, \Leftrightarrow\, \, 0^{\circ}<\alpha <90^{\circ}\cup 180^{\circ}<\alpha <270^{\circ}$
$\displaystyle cot\alpha <0\, \, \, \Leftrightarrow\, \, 90^{\circ}<\alpha <180^{\circ}\cup 270^{\circ}<\alpha <360^{\circ}$
