\[y=senh\, x=\frac{e^{x}-e^{-x}}{2}\]
avente per dominio e codominio l’insieme R dei numeri reali D = R.
\[y=cosh\, x=\frac{e^{x}+e^{-x}}{2}\]
avente per dominio l’insieme R dei numeri reali, D = R, e per codominio l’intervallo $\displaystyle ]1,+\infty [$.
\[y=tanh\, x=\frac{senh\, x}{cosh\, x}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\]
avente per dominio l’insieme D = R, e per codominio l’intervallo ] -1, 1[.
\[y=coth\, x=\frac{cosh\, x}{senh\, x}=\frac{e^{x}+e^{-x}}{e^{x}-e^{-x}}\]
avente per dominio l’insieme D = R – {0}, e per codominio l’intervallo $\displaystyle ]-\infty, -1 [\, \, \, \, \cup \, \, ]1,+\infty [$.
\[y=sech\, x=\frac{1}{cosh\, x}=\frac{2}{e^{x}+e^{-x}}\]
avente per dominio l’insieme D = R e per codominio l’intervallo ( 0,1 ].
\[y=csch\, x=\frac{1}{senh\, x}=\frac{2}{e^{x}-e^{-x}}\]
avente per dominio e codominio l’insieme D = R – {0}.
Nelle seguenti figure sono riportati i grafici delle funzioni iperboliche dirette.
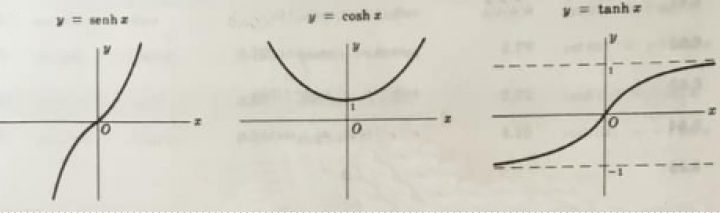
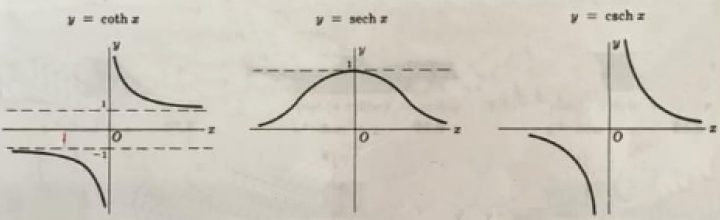
Le funzioni seno e coseno iperbolico sono periodiche di periodo immaginario \[2\pi i\]:\[senh\left ( x+2k\pi i \right )=senhx,\, \, cosh\left ( x+2k\pi i \right )=coshx\] mentre le funzioni tangente e cotangente iperboliche sono periodiche di periodo \[\pi i\]: \[tanh\left ( x+k\pi i \right )=tanhx,\, \, coth\left ( x+k\pi i \right )=cothx\]
Le funzioni iperboliche inverse sono:
\[y=arcsenhx=ln\left ( x+\sqrt{x^{2}+1} \right )\]
avente per dominio e codominio l’insieme R dei numeri reali D = R.
\[y=arccoshx=ln\left ( x+\sqrt{x^{2}-1} \right )\]
avente per dominio D = $\displaystyle [1,+\infty [$ e codominio $\displaystyle [0,+\infty [$ .
\[y=arctanh\, x=ln\left ( \frac{\sqrt{1-x^{2}}}{1-x} \right )=\frac{1}{2}ln\left ( \frac{1+x}{1-x} \right )\]
avente per dominio l’intervallo ] -1, 1 [ e codominio R.
\[y=arccoth\, x=ln\left ( \frac{\sqrt{x^{2}-1}}{1-x} \right )=\frac{1}{2}ln\left ( \frac{x+1}{x-1} \right )\]
avente per dominio l’intervallo $\displaystyle ]-\infty, -1 [\, \, \, \, \cup \, \, ]1,+\infty [$e codominio R – {0}.
\[y=arcsech\, x=ln\left ( \frac{1+\sqrt{1-x^{2}}}{x} \right )\]
avente per dominio l’intervallo (0, 1] e codominio $\displaystyle [0,+\infty [$.
\[y=arccsch\, x=ln\left ( \frac{1\pm \sqrt{1+x^{2}}}{x} \right )\]
avente per dominio l’intervallo R – { 0 } e codominio R – { 0 }.
Ricordiamo che\[arcsenh\, x=sett\, senh\, x=asenh\, x=senh^{-1}x\] e così per le altre funzioni iperboliche inverse.
Nelle seguenti figure sono riportati i grafici delle funzioni iperboliche inverse.
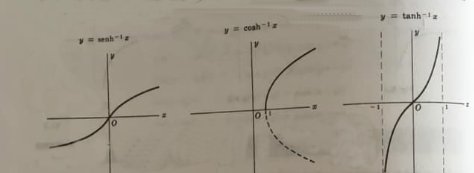
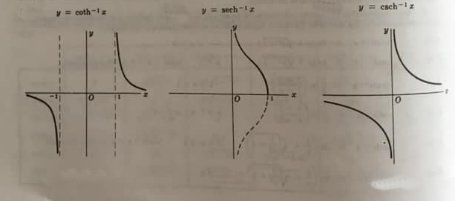
Vediamo come si ricava la funzione iperbolica inversa della funzione senh x (invertibile). Si ha: \[y=senhx=\frac{e^{x}-e^{-x}}{2}=\frac{e^{2x}-1}{2e^{x}}\rightarrow y=\frac{e^{2x}-1}{2e^{x}}\]
da cui \[y\cdot 2\cdot e^{x}=e^{2x}-1\rightarrow 2ye^{x}-e^{2x}+1=0\rightarrow e^{2x}-2ye^{x}-1=0\] e risolvendo l’equazione esponenziale si ha: \[x=ln\left ( y+\sqrt{y^{2}+1} \right )\]
e scambiando x con y si ottiene la funzione inversa \[y=arcsenh\, x=ln\left ( x+\sqrt{x^{2}+1} \right )\]
Analogamente si procede per ricavare le altre funzioni iperoboliche inverse.
Formule relative alle funzioni iperboliche
Relazioni fondamentali
\[tanh\, x=\frac{senh\, x}{cosh\, x},\, \, \, coth\, x=\frac{1}{tanh\, x}=\frac{cosh\, x}{senh\, x}\]
\[sech\, x=\frac{1}{cosh\, x},\, \, \, csch\, x=\frac{1}{senh\, x}\]
\[cosh^{2}x-senh^{2}x=1,\, \, sech^{2}x+tanh^{2}x=1,\, \, coth^{2}x-csch^{2}x=1\]
\[senh\, x+cosh\, x=e^{x},senh\,\, \, x-cosh\, x=-e^{-x}\]
\[1-tanh^{2}x=\frac{1}{cosh^{2}x},\, \, coth^{2}x-1=\frac{1}{senh^{2}x}\]
\[e^{x}=\frac{1+tanh\, \frac{x}{2}}{1-tanh\, \frac{x}{2}}\]
Relazioni tra argomenti negativi
\[senh(-x)=-senhx,\, \, cosh(-x)=coshx,\, \, tanh(-x)=-tanhx,\, \, coth(-x)=-cothx,\, \, sech(-x)=sechx,\, \, csch(-x)=-cschx\]
Formule di addizione e sottrazione
\[senh\left ( x\pm y \right )=senh\, x\, cosh\, y\pm cosh\, x\, senh\, y\]
\[cosh\left ( x\pm y \right )=cosh\, x\, cosh\, y\pm senh\, x\, senh\, y\]
\[tan\, h\left ( x\pm y \right )=\frac{tanh\, x\pm tanh\, y}{1\pm tanh\, x\cdot tanh\, y}\]
\[cot\, h\left ( x\pm y \right )=\frac{cothx\cdot coth\,y\pm 1}{coth\, y\pm coth\, x}\]
Formule di duplicazione
\[senh\, 2x=2\cdot senh\, x\cdot cosh\, x\]
\[cosh\, 2x=senh^{2}\, x+ cosh^{2}\, x=2cosh^{2}x-1=1+2senh^{2}x\]
\[tanh\, 2x=\frac{2tanh\, x}{1+tanh^{2}\, x}\]
Formule di bisezione
\[senh\frac{x}{2}=\pm \sqrt{\frac{coshx-1}{2}},\, \, +se\, x>0,\, -se\, x<0\]
\[cosh\frac{x}{2}= \sqrt{\frac{coshx+1}{2}}\]
\[tanh\frac{x}{2}=\pm \sqrt{\frac{cosh\, x-1}{cosh\, x+1}}=\frac{senhx}{coshx+1}=\frac{coshx-1}{senhx}\]
+ se x > 0 e – se x <0
Potenze delle funzioni iperboliche
\[senh^{2}x=\frac{1}{2}\left ( cosh\, 2x-1 \right ),\, \, cosh^{2}x=\frac{1}{2}\left ( cosh\, 2x+1 \right ),\]
Somma differenza e prodotto tra funzioni iperboliche
\[senhx+senhy=2\cdot senh\frac{x+y}{2}\cdot cosh\frac{x-y}{2}\]
\[senhx-senhy=2\cdot cosh\frac{x+y}{2}\cdot senh\frac{x-y}{2}\]
\[cosh\, x+cosh\, y=2cosh\frac{x+y}{2}cosh\frac{x-y}{2}\]
\[cosh\, x-cosh\, y=2senh\frac{x+y}{2}senh\frac{x-y}{2}\]
\[cosh\, x\cdot cosh\, y=\frac{1}{2}\left [ cosh(x+y)+cosh(x-y) \right ]\]
\[senh\, x\cdot senh\, y=\frac{1}{2}\left [ cosh(x+y)-cosh(x-y) \right ]\]
\[senh\, x\cdot cosh\, y=\frac{1}{2}\left [ senh(x+y)+senh(x-y) \right ]\]
\[tanh\, x\pm tanh\, y=\frac{senh\left ( x\pm y \right )}{cosh\, x\cdot cosh\, y}\]
\[coth\, x+ coth\, y=\frac{senh\left ( x+ y \right )}{senh\, x\cdot senh\, y}\]
\[coth\, x- coth\, y=\frac{senh\left ( y-x \right )}{senh\, x\cdot senh\, y}\]
\[tanh\, x \cdot tanh\, y=\frac{tanh\, x+tanh\, y}{coth\, x+coth\, y}\]
Formule di angoli multipli
\[senh\, 3x=3senh\, x+4senh^{3}\, x\]
\[cosh\, 3x=4cosh^{3}\, x-3cosh\, x\]
\[tanh\, 3x=\frac{3tanh\, x+tanh^{2}\, x}{1+3tanh^{2}\, x}\]
Formule che esprimono tutte le funzioni iperboliche in funzione di una sola di esse
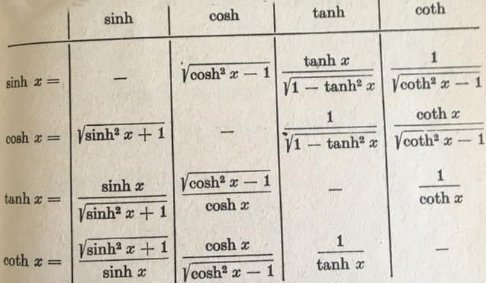
Regola di De Moivre
\[\left ( senhx+coshx \right )^{n}=senh\, nx+cosh\, nx\]
\[\left ( senhx-coshx \right )^{n}=senh\, nx-cosh\, nx\]
Formule relative alle funzioni iperboliche inverse
Espressione delle funzioni iperboliche inverse mediante una sola di esse
\[arcsenh\, x=arcosh\sqrt{x^{2}+1},\, x>0;\, \, arcsenh\, x=-arcosh\sqrt{x^{2}+1},\, x<0\]
\[arcsenh\, x=arctanh\frac{x}{\sqrt{x^{2}+1}}=arccoth\frac{\sqrt{x^{2}+1}}{x}\]
\[arccosh\, x=\pm arcsenh\sqrt{x^{2}-1}=\pm arctanh\frac{\sqrt{x^{2}-1}}{x}=\pm arccoth\frac{x}{\sqrt{x^{2}-1}}\]
\[arctanh\, x=arcsenh\frac{x}{\sqrt{1-x^{2}}}\]
\[arctanh\, x=arcosh\frac{1}{\sqrt{1-x^{2}}},\, x>0;\, \, arctanh\, x=-arcosh\frac{1}{\sqrt{1-x^{2}}},\, x<0\]
\[arctanh\, x=arccoth\frac{1}{x}\]
\[arccoth\, x=arcsenh\frac{1}{\sqrt{x^{2}-1}}\]
\[arccoth\, x=arccosh\frac{1}{\sqrt{x^{2}-1}},x>0;\, \, arccoth\, x=-arccosh\frac{x}{\sqrt{x^{2}-1}},\, x<0\]
\[arccoth\, x=arctan\frac{1}{x}\]
Somma e differenza delle funzioni iperboliche invese
\[arcsenhx\pm arcsenhy=arcsenh\left ( x\sqrt{1+y^{2}}\pm y\sqrt{1+x^{2}} \right )\]
\[arccoshx\pm arccoshy=arccosh\left ( xy\pm \sqrt{\left ( x^{2}-1 \right )\left ( y^{2}-1 \right )} \right )\]
\[arctanhx\pm arctanhy=arctanh\frac{x\pm y}{1\pm xy}\]
