In questa pagina puoi consultare alcuni problemi svolti di massimo e di minimo risolti con i metodi dell’analisi matematica. Altri problemi di massimo e di minimo risolubili senza l’analisi matematica li puoi vedere qui…
Esempio 1.1.- Problemi con i numeri.- La somma di due numeri positivo è 40. Trovare quali numeri rendono massimo il prodotto $\displaystyle x^{3}y^{2}$ .
Esempio 1.2.- Determinare due numeri di somma assegnata e di prodotto massimo. Vedi il mio video
Esempio 2.1.- Problemi di geometria piana.- Tra tutti i rettangoli di diagonale assegnata trovare quello di area massima.
Esempio 2.2.- Fra tutti i rettangoli di perimetro assegnato trovare quello di area massima.
Non lo sai risolvere? Allora vedi il mio video nel mio canale Youtube
Esempio 2.3.- Tra tutti i triangoli rettangoli per i quali è costante la somma di un cateto e dell’ipotenusa trovare quello di area massima.
Esempio 2.4.- Tra tutti i rettangoli rettangoli di assegnata ipotenusa trovare quello di ara massima.
Non lo sai risolvere? Clicca qui
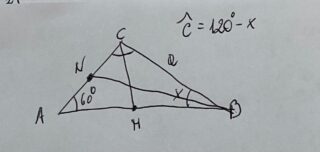
Esempio 2.5.- Dato il triangolo ABC con l’angolo in A di 60 gradi, e il lato opposto al vertice A di misura a>0. Determinare il valore dell’angolo in $\hat{B}=x$ per il quale è massima la somma dei quadrati delle mediane relative ai lati AB e AC.
Risoluzione
Le mediane sono CM e BN. Determinare con il teorema dei seni i lati del triangolo ABC in funzione di x, poi con il teorema del coseno determinare le mediane CM e BN. Quindi scrivere la funzione da massimizzare:
$S(x)=\overline{CM}^{2}+\overline{BN}^{2}=…$
Appliando il teorema dei seni nel triangolo ABC si ha:
$\frac{\overline{AC}}{senx}=\frac{\overline{BC}}{sen60^{\circ}}\rightarrow \overline{AC}=\frac{2a\sqrt{3}sen\: x}{3}$
$\frac{\overline{AB}}{sen\left ( 120^{\circ}-x \right )}=\frac{\overline{BC}}{sen60^{\circ}}\rightarrow \overline{AB}=a\: cosx+\frac{\sqrt{3}}{3}a\cdot senx$
Calcoliamo CM applicando il teorema del coseno nel triangolo ACM e BN applicando il teorema del coseno nel triangolo ABN. Si ha:
$\overline{CM}^{2}=\overline{AC}^{2}+\overline{AM}^{2}-2\overline{AC}\cdot \overline{AM}\, cos60^{\circ}=…$
$\overline{BN}^{2}=\overline{AN}^{2}+\overline{AB}^{2}-2\overline{AN}\cdot \overline{AB}\, cos60^{\circ}=…$
cioè
$\overline{CM}^{2}=\overline{AC}^{2}+\overline{AM}^{2}-\overline{AC}\cdot \overline{AM}\, =…$
$\overline{BN}^{2}=\overline{AN}^{2}+\overline{AB}^{2}-\overline{AN}\cdot \overline{AB}\,=…$
con $\overline{AM}=\frac{\overline{AB}}{2}$ e $\overline{AN}=\frac{\overline{AC}}{2}$.
Sommando membro a membro le due relazioni suddette si ha:
\[ S(x)=\overline{CM}^{2}+\overline{BN}^{2}=\frac{5}{4}\overline{AC}^{2}+\frac{5}{4}\overline{AB}^{2}-\overline{AB}\cdot \overline{AC}\]
e sostituendo i valori di AB e di AC in funzione di x prima trovati si ottiene la funzione S(x) da massimizzare. Si ha:
\[ S(x)=\frac{1}{4}\left [5 \left (2a\frac{\sqrt{3}}{3}senx \right )^{2} +5\left ( acosx+\frac{\sqrt{3}}{3}asenx \right )^{2}-4\left ( 2a\frac{\sqrt{3}}{3}senx \right )\left ( acosx+\frac{\sqrt{3}}{3}asenx \right )\right ]\]
e semplificando
\[ S(x)=\frac{a^{2}}{12}\left ( 17sen^{2}x+15cos^{2}x +2\sqrt{3}senxcosx\right )\]
con l’angolo x compreso tra 0° e 120°.
Calcoliamo la derivata prima trascurando la costante a^2/12 e si ha:
\[ S'(x)=4senxcosx+4\sqrt{3}cos^{2}x-2\sqrt{3}\]
\[ S'(x)=0\to 4senxcosx+4\sqrt{3}cos^{2}x-2\sqrt{3}=0\]
cioè
\[ 2senxcosx+2\sqrt{3}cos^{2}x-\sqrt{3}=0\]
da cui
\[ 2senxcosx+2\sqrt{3}cos^{2}x-\sqrt{3}\left ( cos^{2}x+sen^{2}x \right )=0\]
ossia:
\[ \sqrt{3}sen^{2}x-2sencosx-\sqrt{3}cos^{2}x=0\] ossia
\[ \sqrt{3}tan^{2}x-2tanx-\sqrt{3}=0\]
\[ tanx=\frac{1\pm 2}{\sqrt{3}}\to tanx=-\frac{\sqrt{3}}{3}\cup tanx=\sqrt{3}\]
e risolvendo la seconda equazione goniometrica elementare si ha:
\[ tanx=\sqrt{3}\to x=60^{\circ}\]
Notiamo che:
\[ S(0^{\circ})=\frac{5}{4}a^{2},\, \, \, S(60^{\circ})=\frac{23}{16}a^{2},\, \, \, S(120^{\circ})=\frac{5}{4}a^{2}\]
Esempio 3.1.- Problemi di geometria analitica.- Trovare il punto della reta 4x – y – 1= 0 per il quale è minima la distanza dal punto A(0,3).
Esempio 3.2.- Data la parabola $\displaystyle y=-x^{2}+5$ e indicati con A e B i punti in cui interseca la retta d’equazione y = k determinare k in modo che sia massima l’area della superficie del triangolo OAB, con O origine degli assi cartesiani.
Esempio 3.3.- Determinare il parametro h in modo che la distanza tra i vertici dei seguenti due fasci $\displaystyle y=-2x^{2}+hx+4,\, \, y=2x^{2}+(4-h)x+2h$ di parabole sia massimo. Determinare anche per quale valore di h è minimo, se esiste.
Risoluzione ragionata
Determiniamo prima di tutto i vertici delle due parabole, quindi calcoliamo la distanza tra i due vertici e dunque otteniamo la funzione da massimizzare. Di tale funzione troviamo il valore massimo con l’uso della derivata prima. Si otterrà h= 6.
Esempio 3.4.- Vedi il mio video
Esempio 3.5.- In un sistema di assi coordinati cartesiani si considerino le parabole rispettivamente di equazioni $\displaystyle C’)y=2x-2x^{2},\, \, \, C”)y=x-x^{2}$. Nella regione finita di piano delimitata dalle due curve si conducano:
- La retta di equazione y = k (k >1/4) sulla quale C’ intercetta la corda AB;
- La retta tangente a C” nel suo vertice, sulla quale la parabola C’ intercetta la corda CD.
Determinare per quale valore di k l’area del trapezio ABCD acquisti valore massimo. ( Maturità Scientifica 1978) Se non lo sai risolvere puoi provare qui I Quesiti della Maturità Scientifica
Esempio 3.6.-
Esempio 4.1.- Problemi di trigonometria.- Sulla circonferenza di raggio r determinare l’angolo del vertice A del triangolo ABP per il quale è massima la somma dei quadrati dei lati AP e PB sapendo che l’angolo APB è 60 gradi e il punto P varia sulla circonferenza.
Esempio 4.2.- Si conduca internamente ad un angolo AOB una semiretta OC che formi con OA un angolo AOC = x; presi rispettivamente su OA e su OB due punti M ed N tali che OM = 1 e $\displaystyle ON=\sqrt{3}$ , siano M’ ed N’ le rispettive proiezioni di M ed N su OC. Detto P il medio di M’N’, si determini x in modo che risulti massima l’area del triangolo NOP. (Maturità scientifica 1975)
Esempio 5.1.- Problemi di geometria solida.- Dato un parallelepipedo con uno spigolo di lunghezza 9 e base quadrata di lato x, tale 0 < x < 9. Determinare quale valore di x il parallelepipedo ottenuto sottraendogli il cubo di spigolo x abbia volume massimo.
Esempio 5.2.- Fra tutti i cilindri di uguale superficie S, determinare quello di volume massimo.
Risoluzione ragionata
Indichiamo con x il raggio di base del cilindro. Poi determiniamo l’altezza del cilindro in funzione di x e di S. Infine ricaviamo la funzione volume, di variabile x, e calcoliamo facendo la derivata prima della funzione volume, il valore di x per il quale il volume è massimo.
Esempio 5.3.- Tra tutti i parallelepipedi rettangoli con volume costante e altezza h determinare quello di area laterale minima. Determinare il caso particolare con h = 5.
Esempio 5.4.- Tra tutti i coni inscritti in una sfera di raggio R, determinare quello per il quale è massimo il rapporto tra il suo volume e quello della sfera.
Esempio 5.5.- In un cono circolare retto avente per raggio di base e per altezza rispettivamente i segmenti r ed hr si inscriva il cilindro avente la base sul piano di base del cono ed il volume massimo. Per quale valore di h tale cilindro risulta equilatero? In questo caso particolare si trovi anche il cilindro inscritto per il quale è massima la superficie totale. ( Maturità Scientifica 1976)
Esempio 5.6.- Si determinino l’altezza e il raggio di base del cono di volume minimo circoscritto ad una data sfera di raggio r. Si dimostri poi che il suddetto cono è anche quello di minima superficie totale. ( Maturità Scientifica 1972)
Esempio 6.1.- Problemi di Economia.- La funzione $\displaystyle y=0,008x^{2}+20x-40$ rappresenta un guadagno. Trovare per quale valori di x non si è in perdita e per quale valore di x si ottiene il massimo guadagno. Determinare inoltre il massimo guadagno.
Risoluzione ragionata
Per determinare i valori di x per i quali non si è in perdita bisogna determinare i valori di x per i quali la parabola è situata non al di sotto dell’asse x, ovvero i punti x per i quali y è non negativa. Il punto di massimo della funzione si ottiene annullando la derivata prima della funzione. Il guadagno è massimo per x = 1250.
Esempio 6.2.- Una azienda agricola produce olio con costi fissi pari a 1000 euro e costi variabili secondo la quantità p di litri d’olio prodotti espressi dalla formula $\displaystyle C\left ( p \right )=12p^{2}-960p$. Il ricavo invece rispetto alla quantità di merce venduta è dato da $\displaystyle R\left ( v \right )=10v^{2}$ . Supponendo di vendere tutto l’olio prodotto trovare il numero di litri d’olio per ottenere il guadagno massimo. Calcolare anche il guadagno massimo ottenuto.
Risoluzione ragionata
Numero litri d’olio = 240
Esempio 7.1.- Problemi di fisica.- Una spira quadrata di lato 0,5 metri è immersa in un campo magnetico uniforme che forma un angolo di 30 gradi con la normale al piano della spira. Il modulo del campo magnetico misurato in Tesla varia nel tempo (in secondi) con la seguente legge B(t)=t(e^-(t^2)), con t maggiore uguale di zero. Determina in quale istante il flusso magnetico attraverso la superficie della spira è massimo. Calcolare tale valore massimo. Quanto vale la forza elettromotrice indotta nella spira all’istante determinato?
Esempio 8.1.- Problemi reali.- Fra tutti i recipienti di forma cilindrica di uguale superficie S, determinare quello di volume massimo.