 Argomenti propedeutici:
Argomenti propedeutici:
- Grafico di una funzione
- Teorema degli zeri e funzioni continue
- Metodo di bisezione
- Teorema fondamentale dell’algebra
- Derivata di una funzione e funzione monotóna
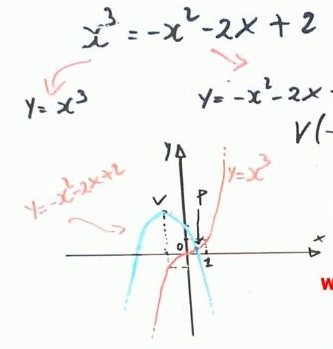
Esempio 1.- Risolvere la seguente equazione \[x^{3}+x^{2}+2x-2=0\]
Se non sai come fare non disperare! Vedi il mio video nel mio canale Youtube.
Esempio 2.- Risolvere la seguente equazione \[x^{3}-16x^{2}-19x+34=0\]
Suggerimento.- L’utente che sa studiare le funzioni può cominciare ad intuire il grafico della funzione \[y=x^{3}-16x^{2}-19x+34\] con la semplice analisi della derivata prima e il calcolo dei limiti all’infinito
Se non sai come fare non disperare! Vedi il mio video nel mio canale Youtube.
NOTA.- L’equazione assegnata si potrebbe risolvere anche con l’uso del Teorema di Ruffini, ma qui vogliamo farlo con l”uso del teorema degli zeri.
Esempio 3.- Risolvere la seguente equazione \[x^{3}-18x^{2}+15x+34=0\]
Esempio 4.- Risolvere la seguente equazione \[x^{3}-10x^{2}-27x+36=0\]
Esempio 5.- Risolvere la seguente equazione \[x^{3}+x+1=0\] e trovare la soluzione con un errore più piccolo di 0,01.
Esempio 6.- Verificare che la seguente equazione \[-x^{3}-x^{2}+1=0\] ammette una soluzione nell’intervallo [ 0, 1 ] e trovare la soluzione con un errore più piccolo di 0,01.
Esempio 7.- Risolvere la seguente equazione \[x^{4}-20x-25=0\]
Risultato: x = -1,1596, x = 3,0442
Esempio 8.- Risolvere la seguente equazione \[e^{x}+x-2=0\]
Risultato: 0 < x < 1
Esempio 9.- Risolvere la seguente equazione \[lnx+2x-3=0\]
Risultato: x = 1,349
Esempio 10.- Risolvere la seguente equazione \[senx-2x-1=0\]
Risultato: x = – 0,887
Esempio 11.- Risolvere la seguente equazione \[x^2=2^x\]
Non sai risolvere l’esercizio? Allora prova a vedere il mio video su Youtube
La funzione di Lambert, introdotta verso la fine del video, è una funzione complessa di variabile complessa con più rami, riguarda dunque l’analisi matematica superiore. Tale funzione non si utilizza normalmente nei programmi della Scuola Superiore o degli esami di matematica dei corsi base dell’Università.
