Se hai difficoltà con lo studio di una funzione comincia con quelle delle scuole superiori.
Esempio 1.- Studiare la seguente funzione e accennare il grafico \[y=\sqrt{x^{2}-1}\cdot e^{\frac{x+1}{x-1}}\]
Il dominio D si ottiene richiedendo \[\left\{\begin{matrix} x^{2}-1 &\geq 0 \\ x-1 &\neq 0 \end{matrix}\right.\] ed è \[D=(-\infty ,-1]\cup \left ( 1,+\infty \right )\]
La funzione è sempre positiva e nulla in x = -1.
La derivata prima è\[f'(x)=e^{\frac{x+1}{x-1}}\cdot \frac{\left ( x-1 \right )\left ( x^{2}-3x-2 \right )}{\sqrt{x^{2}-1}\left ( x-1 \right )^{2}}\]
e la disequazione \[f'(x)\geq 0\Rightarrow (x-1)\left ( x^{2}-3x-2 \right )\geq 0\]
è verificata nel dominio per \[x\geq \frac{3+\sqrt{17}}{2}\] e dunque la funzione ammette un minimo in x = 1 e un minimo in \[x=\frac{3+\sqrt{17}}{2}\]
Inoltre la funzione ammette un asintoto verticale in x = 1 e un asintoto obliquo d’equazione y =ex+2e a più infinito e un altro a meno infinito d’equazione y = -ex-2e.
Esempio 2.1.- Studiare la seguenti funzioni e accennare il grafico $\displaystyle f(x)=x-2arctan\, x$
\[y=\frac{x^{2}}{16}(4ln^{2}\frac{x}{4}-10ln\frac{x}{4}+5)\]
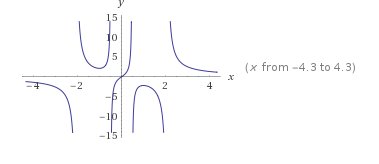
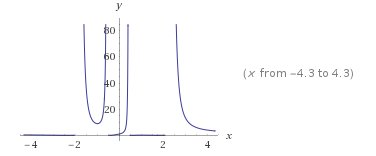
Esempio 2.2.- Studiare la seguente funzione e accennare il grafico \[y=e^{tan\left ( \frac{4x}{1+x^{2}} \right )}\]
Il dominio D della funzione si ottiene imponendo \[\frac{4x}{1+x^{2}}\neq \frac{\pi }{2}+k\pi ,\, \, \, k\in Z\] ed è \[x\neq \frac{2\pm\sqrt{4-\frac{\pi ^{2}}{4}} }{\pm \frac{\pi }{2}}\]
La funzione è sempre positiva e interseca l’asse y nel punto (0, 1).
La derivata prima è \[f'(x)=e^{tan\left ( \frac{4x}{1+x^{2}} \right )}\left ( 1+tan^2\frac{4x}{1+x^{2}} \right )\frac{(-4x^{2}+4)}{\left ( 1+x^{2} \right )^{2}}\]
e risolvendo la disequazione \[f'(x)\geq 0\Rightarrow -4x^{2}+4\geq 0\Rightarrow -1\leq x\leq 1\] si stabilisce che la funzione ammette un minimo relativo in x= -1 e un massimo relativo in x = 1 con
\[f(1)=e^{tan2},\, \, \, \, f(-1)=e^{-tan2}\]
La funzione ammette quattro asintoti verticali d’equazione \[x= \frac{2\pm\sqrt{4-\frac{\pi ^{2}}{4}} }{\pm \frac{\pi }{2}}\] e l’asintoto orizzontale d’equazione y =1.
Esempio 3.- Studiare la seguente funzione e accennare il grafico probabile \[y=sen\left ( \frac{5x^{2}+1}{x^{4}+1} \right )\]
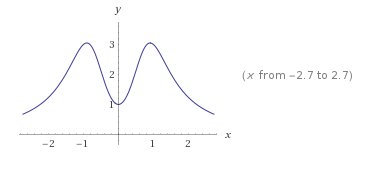
Conviene studiare prima la funzione pari \[f(x)=\frac{5x^{2}+1}{x^{4}+1}\] e poi dedurre il grafico probabile della funzione assegnata
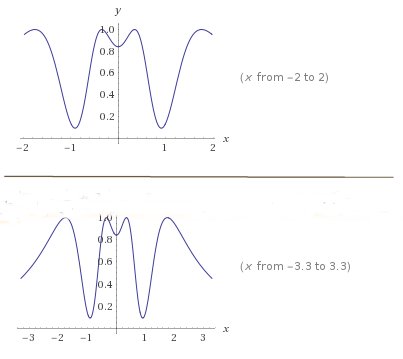
La funzione è definita in R, è pari e positiva, interseca l’asse y nel punto (0,1) e ammette come asintoto orizzontale la retta y = 0.
La derivata prima è\[f'(x)=\frac{10x\left ( x^{4}+1 \right )-4x^{3}\left ( 5x^{2}+1 \right )}{\left ( x^{4}+1 \right )^{2}}=-\frac{2x\left ( 5x^{4}+2x^{2}-5 \right )}{\left ( x^{4}+1 \right )^{2}}\]
e risolvendo \[f'(x)=-\frac{2x\left ( 5x^{4}+2x^{2}-5 \right )}{\left ( x^{4}+1 \right )^{2}}\geq 0\]
si vede che la funzione ammette un minimo relativo in x = 0 e due massimi relativi in \[x=\pm \sqrt{\frac{-1+\sqrt{26}}{5}}\approx \pm 0,9\]
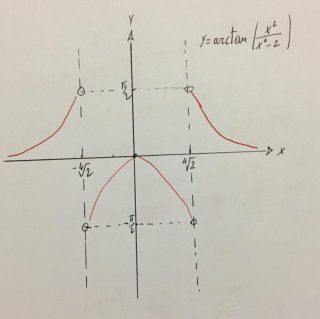
Esempio 4.- Studiare la seguente funzione e accennare il grafico \[y=arctan\left ( \frac{x^{2}}{x^{4}-2} \right )\]
Il dominio della funzione si ottiene richiedendo che \[x^{4}-2\neq 0\Rightarrow x\neq \pm \sqrt[4]{2}\]
e quindi il dominio è \[D= R-\left \{ \pm \sqrt[4]{2} \right \}\]
Studiamo il segno della funzione risolvendo la disequazione \[y\geq 0\Rightarrow arctan\left ( \frac{x^{2}}{x^{4}-2} \right )\geq 0\Rightarrow \frac{x^{2}}{x^{4}-2}\geq 0\]
Risolta tale disequazione fratta si vede che la funzione è positiva per \[x\leq -\sqrt[4]{2},\, \, \, x\geq \sqrt[4]{2}\] e interseca gli assi in O(0,0) e negativa altrimenti.
Dall’essere \[\lim_{x\rightarrow \sqrt[4]{2}\, ^{+}}arctan\left ( \frac{x^{2}}{x^{4}-2} \right )=\frac{\pi }{2}\]
e \[\lim_{x\rightarrow \sqrt[4]{2}\,\, ^{-}}arctan\left ( \frac{x}{x^{4}-2} \right )=-\frac{\pi }{2}\]
si deduce che i punti \[P(\sqrt[4]{2},\frac{\pi }{2})\] e \[P'(\sqrt[4]{2},-\frac{\pi }{2})\]
sono punti di discontinuità di prima specie; mentre dall’essere
\[\lim_{x\rightarrow- \sqrt[4]{2}\,\, ^{+}}arctan\left ( \frac{x}{x^{4}-2} \right )=-\frac{\pi }{2}\]
\[\lim_{x\rightarrow- \sqrt[4]{2}\,\, ^{-}}arctan\left ( \frac{x}{x^{4}-2} \right )=\frac{\pi }{2}\]
si deduce che i punti \[Q(-\sqrt[4]{2},\frac{\pi }{2})\]
\[Q'(-\sqrt[4]{2},-\frac{\pi }{2})\] sono di discontinuità di prima specie.
Infine dall’essere \[\lim_{x\rightarrow \pm \infty }arctan\left ( \frac{x^{2}}{x^{4}-2} \right )=0\] si deduce che l’asintoto orizzontale è l’asse x, y = 0.
La derivata prima è \[y’=\frac{1}{1+\left ( \frac{x^{2}}{x^{4}-2} \right )^{2}}\cdot \frac{2x\left ( x^{4}-2 \right )-x^{2}(4x^{3})}{\left ( x^{4}-2 \right )^{2}}=\frac{1}{1+\left ( \frac{x^{2}}{x^{4}-2} \right )^{2}}\frac{2x^{5}-4x-4x^{5}}{\left ( x^{4}-2 \right )^{2}}=\frac{1}{1+\left ( \frac{x^{2}}{x^{4}-2} \right )^{2}}\frac{-4x-2x^{5}}{\left ( x^{4}-2 \right )^{2}}\]
Risolvendo \[y’=\frac{1}{1+\left ( \frac{x^{2}}{x^{4}-2} \right )^{2}}\frac{-4x-2x^{5}}{\left ( x^{4}-2 \right )^{2}}\geq 0\Rightarrow -4x-2x^{5}\geq 0\Rightarrow -2x(2+x^{4})\geqslant 0\Rightarrow x\leq 0\]
si deduce che la funzione ammette un massimo relativo nel punto x = 0, M(0,0).
Il grafico della funzione è rappresentato nella seguente figura:
Esempio 5.- Studiare la seguente funzione e accennare il grafico \[y=tan\left ( e^{\frac{4x}{1+x^{2}}} \right )\]
Esempio 5.1. – Studiare la seguente funzione e accennare il grafico\[f(x)=xe^{\frac{x+1}{x-1}}\]
Esempio 6.- Studiare la seguente funzione e accennare il grafico \[y=\sqrt{1+\left ( \frac{x^{2}-3x+2}{x+1} \right )^{2}}\]
Esempio 6.1.- Studiare la seguente funzione e accennare il grafico
\[ f(x)=\sqrt[3]{\left(x-1\right)^{2}(x-2)}\]
Risoluzione
Dominio R, intersezione con l’asse x in x = 1, x = 2; intersezione con l’asse y in $-\sqrt[3]{2}$. Positiva per x > 2, negativa per x <2. Nessun asintoto verticale o orizzontale, ma un asintoto obliquo y = x – 4/3; intersezione con l’asintoto in (10/9, -2/9)… Non sai fare lo studio di questa funzione? Vedi il mio video…
Esempio 7.- Studiare la seguente funzione e accennare il grafico \[y=\left | \frac{\left ( x-1 \right )^{2}}{x+1} \cdot arctanx\right |\]
Esempio 8.- Studiare la seguente funzione e accennare il grafico\[y=sen\left ( \frac{10}{x^{2}+1} \right )\]
Esempio 9.- Studiare la seguente funzione e accennare il grafico \[y=ln\left ( 1+sen\left ( \frac{2x}{x^{2}+1} \right ) \right )\]
Esempio 10.- Studiare la seguente funzione e accennare il grafico \[y=x\cdot sen\left ( \frac{3x}{1+x^{2}} \right )\]
Esempio 11.- Studiare la seguente funzione e accennare il grafico \[y=\left ( x+1 \right )arctan\left ( \left | x^{2}-1 \right | \right )\]
Esempio 12.- Studiare la seguente funzione e accennare il grafico \[y=\left | x^{2}-1 \right |arctan\left ( \frac{1}{x+1} \right )\]
Esempio 13.- Studiare la seguente funzione e accennare il grafico \[y=x^{2}\cdot ln\left ( \frac{x^{2}-x+1}{x^{2}+x+1} \right )\]
Il dominio è l’insieme R dei numeri reali.
Esempio 14.- Studiare la seguente funzione e accennare il grafico \[y=\left | x \right |cos\left ( \frac{x}{x^{2}+1} \right )\]
La funzione è definita in R e si può scrivere, togliendo il modulo, nel seguente modo:
\[y=\left\{\begin{matrix} x\cdot cos\left ( \frac{x}{x^{2}+1} \right ) & se\, x\geq 0\\ -x\cdot cos\left ( \frac{x}{x^{2}+1} \right ) & se\, x<0 \end{matrix}\right.\]
Esempio 15.- Studiare la seguente funzione e accennare il grafico \[y=arccos\left ( \frac{x^{2}-1}{x^{2}+1} \right )\]
Esempio 16.- Studiare la seguente funzione e accennare il grafico \[y=arctan\left ( \frac{\left | x \right |}{x+1} \right )\]
La funzione è definita in R – { -1} e si può scrivere nel seguente modo\[f(x)=\left\{\begin{matrix} arctan\left ( \frac{x}{x+1} \right ) & se\, \geq 0\\ arctan\left ( \frac{-x}{x+1} \right ) & se\: x<0,\, x\neq -1 \end{matrix}\right.\]
Studiamo separatamente le due funzioni:
\[f_{1}(x)=arctan\left ( \frac{x}{x+1} \right )\, \, se\, x\geq 0\]
\[f_{2}(x)=arctan\left ( \frac{-x}{x+1} \right )\, \, se\, x< 0,x\neq -1\]
La funzione \[f_{1}(x)\] passa per il punto O(0,0) è sempre positiva ed ha un asintoto orizzontale \[y=\frac{\pi }{4}\] a più infinito. La derivata prima è sempre positiva.
La funzione \[f_{2}(x)\] ha un punto di discontinuità di prima specie in x = -1
\[\lim_{x\rightarrow -1^{+}}arctan\left ( \frac{-x}{x+1} \right )=\frac{\pi }{2}\]
\[\lim_{x\rightarrow -1^{-}}arctan\left ( \frac{-x}{x+1} \right )=-\frac{\pi }{2}\]
ha un asintoto orizzontale \[y=-\frac{\pi }{4}\]
a meno infinito, è positiva per -1 < x < 0 e negativa per x < -1, inoltre tende a zero per x che tende a zero. La derivata prima è sempre negativa e la derivata seconda si annulla in x = -1/2, punto di flesso \[F\left ( -\frac{1}{2} ,\frac{\pi }{4}\right )\]
Il grafico della funzione f(x) è l’unione dei grafici delle due funzioni \[f_{1}(x),\, \, f_{2}(x)\]
Nell’origine O la funzione f(x) presenta un punto angoloso con tangente destra y = x e sinistra y = -x.
Un altro modo di studiare la funzione era quello di tracciare il grafico della componente interna\[g(x)=\frac{\left | x \right |}{x+1}\] e poi dedurre il grafico della funzione \[f(x)\] in base alle proprietà della componente interna e della componente esterna.
Esempio 17.- Studiare la seguente funzione e accennare il grafico \[y=ln\left ( \left | \frac{x+1}{x} \right | \right )\cdot \frac{x^{3}-x+1}{x+3}\]
Esempio 18.- Studiare la seguente funzione e accennare il grafico \[f(x)=\sqrt{x(x+1)}\cdot exp\left ( \frac{x+1}{x^{2}+1} \right )\]
Esempio 19.- Studiare la seguente funzione e accennare il grafico \[f(x)=\sqrt{\frac{x^{4}}{x^{2}-1}}\cdot exp\left ( \frac{-1}{x^{2}-1} \right )\]
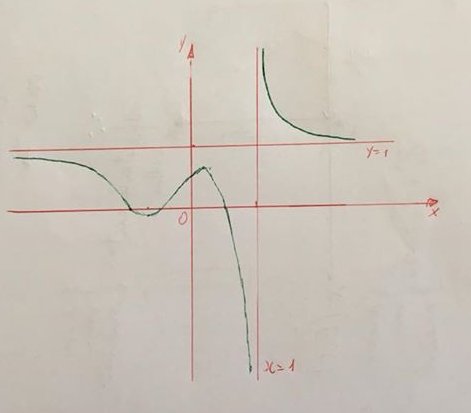
Esempio 20.- Studiare la seguente funzione e accennare il grafico \[f(x)=\frac{x+1}{x-1}cos\left ( \frac{2}{x^{2}+1} \right )\]
La funzione è definita in \[D=R-\left \{ 1 \right \}\] e ammette come asintoto verticale la retta x = 1 e come asintoto orizzontale la retta y = 1. La derivata prima è
\[f'(x)=\frac{2\left [ \left ( x^{2}+1 \right )^{2}cos\left ( \frac{2}{1+x^{2}} \right )+2x\left ( 1-x^{2} \right )sen\left ( \frac{2}{1+x^{2}} \right ) \right ]}{\left ( x-1 \right )^{2}\left ( x^{2}+1 \right )^{2}}\]
e non si può studiare elementarmente, però osservato che la funzione interseca l’asse x in tre punti \[x=-1,\, \, \, x=-\sqrt{\frac{4}{\pi }-1},\, \, \, \, x=\sqrt{\frac{4}{\pi }-1}\]
ottenuti risolvendo l’equazione
\[\frac{x+1}{x-1}\, cos\left ( \frac{2}{x^{2}+1} \right )=0\]
applicando il teorema di Rolle si deduce che la funzione ammette almeno due punti in cui la derivata prima si annulla appartenenti agli intervalli:
\[\left (-1,\, \, \, -\sqrt{\frac{4}{\pi }-1} \right ),\, \, \, \, \left (-\sqrt{\frac{4}{\pi }-1},\sqrt{\frac{4}{\pi }-1} \right )\]
e con il metodo di bisezione si può vedere che tali punti sono approssimativamente \[x=-0,7,\, \, \, \, \, \, x=0,2\].
Dalle informazioni ottenute si può accennare il grafico della funzione
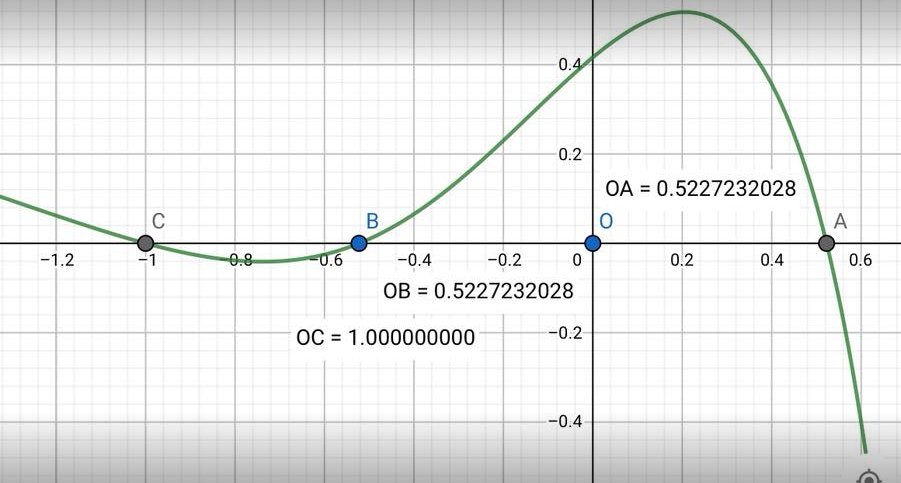
Nel grafico seguente ottenuto con Geogebra si possono vedere meglio i punti di massimo e minimo locali.
Esempio 21.- Studiare la seguente funzione e accennare il grafico \[f(x)=exp\left ( \frac{\left | x^{3}-1 \right |}{\left | x \right |^{3}+1} \right )\]
Dominio: \[\left | x \right |^{3}+1\neq 0\Rightarrow \forall x\in R\]
La funzione si può scrivere nel seguente modo:
\[f(x)=\left\{\begin{matrix} exp\left ( \frac{1-x^{3}}{-x^{3}+1} \right ) &\, se \, \, x\leq 0 \\ exp\left ( \frac{1-x^{3}}{x^{3}+1} \right ) &\, se\, 0<x<1 \\ exp\left ( \frac{x^{3}-1}{x^{3}+1} \right ) &\, se\, x\geq 1 \end{matrix}\right.\]
Positività: funzione sempre positiva
Limiti e asintoti: la curva ammette un asintoto orizzontale a più infinito e non presenta discontinuità
Derivata prima: per 0 < x < 1 la derivata prima è: $\displaystyle y’=\frac{-6x^{2}exp\left ( \frac{1-x^{3}}{1+x^{3}} \right )}{\left ( 1+x^{3} \right )^{2}}$
Derivata seconda: la derivata seconda si annulla per 0 < x < 1 e dunque la funzione ammette un flesso,
Esempio 22.- Studiare la seguente funzione e accennare il grafico \[f(x)=\left | x^{2}-1\right |e^{-x}\]
Non sai studiare una funzione?
Prova a studiare sul mio libro “Lo studio di una funzione“

