Calcolo di un limite con la formula di Taylor con il resto di Peano

Argomenti propedeutici:

1. Sviluppi in serie di una funzione con la formula di Taylor e il resto di Peano;
2. Svluppi in serie di alcune funzioni elementari
3. Calcolo di un limite con la formula di Taylor con il resto di Peano
4. Algebra degli o-piccolo.
5. Primi esercizi

Esempio 1.- Calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{arctan\left ( \frac{x-x^{2}}{1+2x} \right )+ln\left ( \frac{1+2x}{1+x^{2}} \right )-sen\left ( \frac{3x-x^{2}}{1+x} \right )}{arsen\left ( \frac{x-x^{2}}{1+x^{2}} \right )exp\left ( \frac{x+x^{2}}{1+x} \right )arctan\left ( \frac{x+x^{2}}{1-x^{2}} \right )}\]

Risoluzione

Cominciamo a sviluppare al denominatore la funzione \[arcsen\left (\frac{x-x^{2}}{1+x^{2}} \right )\] e precisamente prima la funzione \[\frac{x-x^{2}}{1+x^{2}}\]. Si ha:

\[\frac{x-x^{2}}{1+x^{2}}=\left ( x-x^{2} \right )\frac{1}{1+x^{2}}=\left ( x-x^{2} \right )\left ( 1-x^{2}+o(x^{2}) \right )=x+o(x)\]

Quindi posto \[t=x+o(x)\] sviluppiamo la funzione arcoseno e si ha \[arcsen\left ( x+o(x) \right )=x+o(x)+o\left ( x+o(x)) \right )=x+o(x)\]

Per quanto riguarda invece la funzione esponenziale al denominatore si ha:\[exp\left ( \frac{x+x^{2}}{1+x} \right )=1+o(1)\]

e per la funzione \[arctan\left ( \frac{x+x^{2}}{1-x^{2}} \right )\] si ha prima \[\frac{x+x^{2}}{1-x^{2}} =\left ( x+x^{2} \right )\frac{1}{1-x^{2}}=\left ( x+x^{2} \right )\left ( 1+x^{2}+o(x^{2}) \right )=x+o(x)\]
e poi \[arctan\left ( x+o(x) \right ) =x+o(x)\]

Al numeratore invece si ha:

\[arctan\left ( \frac{x-x^{2}}{1+2x} \right ) =x-3x^{2}+o(x^{2})\]

\[ln\left ( \frac{1+2x}{1+x^{2}} \right ) =2x-3x^{2}+o(x^{2})\]

\[sen\left ( \frac{3x-x^{2}}{1+x} \right ) =3x-4x^{2}+o(x^{2})\]

In base a tali sviluppi il limite assegnato si può scrivere nel seguente modo e vale -2: \[\lim_{x\rightarrow 0}\frac{-2x^{2}+o(x^{2})}{x^{2}+o(x^{2})}=-2\]

Analogamente si procede per calcolare i limiti degli esempi seguenti.

Esempio 2.- Calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{tan\left ( \frac{x}{1-x} \right )+ln\left ( \frac{1-x}{1+x} \right )+cos\left ( \frac{2x}{1+x^{2}} \right )-exp\left ( \frac{-x}{x+1} \right )}{tan\left ( \frac{x^{2}}{1+x^{2}} \right )\cdot arctan\left ( \frac{1-x^{2}}{x^{2}} \right )}\]

Esempio 3.- Calcolare il seguente limite \[\lim_{x\rightarrow -\infty}\frac{\sqrt{x^{2}+x}-xe^{\frac{1}{x+2}}-2cos\frac{2}{1+x}}{arctan\frac{x-1}{x+2}\cdot sen\frac{-1}{2x+1}}\]

Esempio 4.- Calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{tan\frac{x+x^{2}}{1-x}+ln\frac{1+x}{1+2x^{2}}-sinh\frac{2x}{x+1}}{ln\frac{1+2x}{x^{2}+1}\cdot sin\frac{2x}{2x^{2}+1}}\]

Esempio 5.- Calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{e^{\frac{x+2x^{2}}{2-x^{2}}}-sin\frac{x^{2}+x}{2-x^{2}}-cos\frac{2x+x^{2}}{1-2x^{2}}}{ln\frac{2x^{2}+x}{-x^{3}+x}\cdot tan\frac{2x^{3}+x}{-x^{2}+1}}\]

Esempio 6.- Calcolare il seguente limite

\[\lim_{x\rightarrow 0}\frac{tan\left ( \frac{x+x^{2}}{1-x} \right )+exp\left ( \frac{x-x^{2}}{1+x} \right )-ln\left ( \frac{1+2x}{1+x} \right )-cos\left ( \frac{x+x^{2}}{1-x} \right )}{arctan\left (\frac{x-x^{2}}{1+2x} \right )\cdot ln\left (\frac{1+2x}{1-x} \right )}\]

Esempio 7.- Calcolare il seguente limite

\[\lim_{x\rightarrow 0}\frac{ln\left ( \frac{4+3x}{4-x} \right )+cosh\left ( \frac{x+2x^{2}}{1-x} \right )-exp\left ( \frac{x-3x^{2}}{1+3x} \right )}{sen\left (\frac{x+2x^{2}}{2+x} \right )\cdot exp\left (\frac{3x-x^{2}}{x+3x^{2}} \right )\cdot arctan\left ( \frac{2x-x^{2}}{1+2x} \right ) }\]

Esempio 8.- Calcolare il seguente limite

\[\lim_{x\rightarrow 0}\frac{ln\left ( \frac{2+x}{2-x} \right )+cosh\left ( \frac{x}{1-x} \right )-e^{\frac{x}{1+x}}}{arctan\left ( \frac{x-x^{2}}{1+x^{3}} \right )ln\left ( \frac{3+x}{3-x} \right )e^{\frac{x+x^{2}}{x-x^{2}}}}\]

Esempio 9.- Calcolare il seguente limite

$\displaystyle \lim_{x\rightarrow +\infty }\frac{ln\left ( \frac{2+x}{x-1} \right )-cos\left ( \frac{x+1}{1+x^{2}} \right )+exp\left ( \frac{-2x}{1+x^{2}} \right )-arcsin\left ( \frac{x}{x^{2}+1} \right )}{tan\left ( \frac{x+2}{x^{2}+1} \right )\cdot tanh\left ( \frac{x^{2}+2}{x+1} \right )\cdot arctan\left ( \frac{x+1}{x^{2}+2} \right )}$

Il limite vale zero.

Esempio 10.- Calcolare il seguente limite

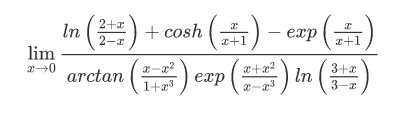
Il risultato è $\frac{3}{2e}$.

Esempio 11.- Calcolare il seguente limite

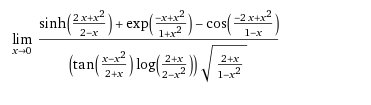
Il risultato è $9\sqrt{2}$.

Esempio 12.- Calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\frac{-ln\left ( \frac{x^{2}+2x}{x^{2}-1} \right )+exp\left ( \frac{x-1}{x^{2}+2x} \right )+1-2cos\left ( \frac{\sqrt{x}}{x^{2}+1} \right )}{sen\left ( \frac{x+1}{x^{2}-1} \right )exp\left (\frac{2x+1}{x-2} \right )arctan\left ( \frac{x-1}{x^{2}+1} \right )}\]

Esempio 13.- Calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\frac{arctan\frac{x^{2}+1}{x+1}-\frac{\pi}{2}\left [ exp\left ( \frac{x+1}{x+2} \right )+ln\left ( \frac{x+2}{x+1} \right ) \right ]+senh\frac{x}{x^{2}+3}}{arcsen\frac{x+1}{x^{3}+5}\cdot\, arctan\frac{x^{3}+1}{x+3} }\]

Il limite vale $-\left ( \frac{2}{\pi }+3 \right )$.

Esempio 14.- \[\lim_{x\rightarrow 0}\frac{tan\left ( \frac{x+x^{2}}{1-x} \right )+exp\left ( \frac{x-x^{2}}{1+x} \right )-ln\left ( \frac{1+3x}{1+x} \right )-cos\left ( \frac{x+x^{2}}{1-x} \right )}{arctan\left ( \frac{x-x^{2}}{1+2x} \right )ln\left ( \frac{1++2x}{1+x} \right )}\]

Risultato: 5/3

Esempio 15.- Calcolare il seguente limite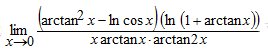

Il limite vale 3/4. Tale limite si può calcolare anche con l’uso dei limiti notevoli.

Esempio 16.- Calcolare il seguente limite 

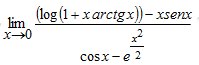
Il limite vale 0. Tale limite si può calcolare anche con l’uso dei limiti notevoli.

Esempio 17.- Calcolare il seguente limite 

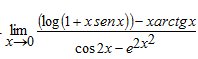
Il limite vale 0. Tale limite si può calcolare anche con l’uso dei limiti notevoli.

Esempio 18.- Calcolare il seguente limite\[\displaystyle \lim_{ x\to +\infty }\frac{a-b+c}{d\cdot m\cdot g}\]

con

\[a=cos\left ( \frac{2}{x+1} \right )\]

\[b=e^{\frac{x+1}{x^{2}+2}}\]

\[c=ln\left ( \frac{2x-1}{2x+1} \right )\]

\[d=ln\left ( \frac{x+2}{x-2} \right )\]

\[m=e^{\frac{2x-1}{2x+1}}\]

\[g=arctan\left ( \frac{x+3}{x^{2}+1} \right )\]