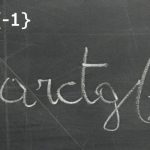 Studiare le seguenti funzioni e tracciare il grafico. Gli esempi dispari sono stati assegnati alla prova di matematica della facoltà di Biologia, i pari alla facoltà di Economia.
Studiare le seguenti funzioni e tracciare il grafico. Gli esempi dispari sono stati assegnati alla prova di matematica della facoltà di Biologia, i pari alla facoltà di Economia.
Se hai difficoltà con lo studio di una funzione comincia con quelle delle scuole superiori
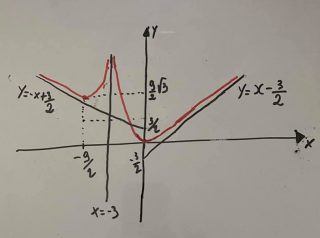
Esempio 1.- Studiare la seguente funzione e accennare il grafico \[f(x)=\sqrt{\frac{x^{3}}{x+3}}\]
Per determinare il dominio D della funzione occorre richiedere che il radicando sia maggiore o uguale di zero, ossia \[\frac{x^{3}}{x+3}\geq 0\]
La funzione è sempre positiva e si annulla in x =0; inoltre ammette un asintoto verticale x = -3 e un asintoto obliquo $\displaystyle y=x-\frac{3}{2}$ a più infinito e un asintoto obliquo a meno infinito $\displaystyle y=-x+\frac{3}{2}$.
\[m=\displaystyle \lim_{x \to +\infty }\frac{\sqrt{\frac{x^{3}}{x+3}}}{x}=1,q=\displaystyle \lim_{x \to +\infty }\left ( \sqrt{\frac{x^{3}}{x+3}}-x \right )=-3/2\]
\[m=\displaystyle \lim_{x \to -\infty }\frac{\sqrt{\frac{x^{3}}{x+3}}}{x}=-1,q=\displaystyle \lim_{x \to -\infty }\left ( \sqrt{\frac{x^{3}}{x+3}}-x \right )=3/2\]
La derivata prima è \[f'(x)=\frac{1}{2\sqrt{\frac{x^{3}}{x+3}}}\frac{3x^{2}(x+3)-x^{3}}{\left ( x+3 \right )^{2}}=\frac{x^{2}\left ( 2x+9 \right )}{2\left ( x+3 \right )^{2}\sqrt{\frac{x^{3}}{x+3}} }\] e la funzione ammette due minimi in x = 0 e x = – 9/2
Esempio 2.- Studiare la seguente funzione e accennare il grafico\[f(x)=\sqrt{x^{3}-4x^{2}}\]
Per determinare il dominio D della funzione occorre richiedere che il radicando sia maggiore o uguale di zero, ossia \[x^{3}-4x^{2}\geq 0\] ed è definita in \[D=\left \{ 0 \right \}\cup [4,+\infty )\] e positiva o nulla nel dominio, si annulla in x = 0 e x = 4. La derivata prima è \[f'(x)=\frac{x\left ( 3x-8 \right )}{2\sqrt{x^{3}-4x^{2}}}\] e la funzione ammette un minimo assoluto nel punto x = 4. Il grafico della funzione è riportato nella figura
Esempio 3.- Studiare la seguente funzione e accennare il grafico\[f(x)=\frac{e^{x}+1}{e^{x}-1}\]
Esempio 4.- Studiare la seguente funzione e accennare il grafico\[f(x)=2+\sqrt{\frac{x}{e^{x}}}\]
Non riesci a studiare la funzione? Allora vedi il mio video su Youtube
Esempio 5.- Studiare la seguente funzione e accennare il grafico\[f(x)=(x+1)e^{\frac{x}{x-1}}\]
Esempio 6.- Studiare la seguente funzione e accennare il grafico\[f(x)=120x^{2}e^{-\left | x \right |}-1\]
Esempio 7.- Studiare la seguente funzione e accennare il grafico\[f(x)=2x-arcsenx\]
Esempio 8.- Studiare la seguente funzione e accennare il grafico \[f(x)=\left\{\begin{matrix} \left ( 3+lnx \right )lnx &\, \, dove\, \, ha\, \, \, significato\\ 0 & se \, \, x = 0 \end{matrix}\right.\]
Esempio 9.- Studiare la seguente funzione e accennare il grafico\[f(x)=ln(1+2sen^{2}x)\]
Esempio 10.- Studiare la seguente funzione e accennare il grafico\[f(x)=ln\left ( \sqrt{5}+e^{-x^{2}} \right )\]
Esempio 11.- Studiare la seguente funzione e accennare il grafico\[f(x)=(x^{2}+2x)e^{x}\]
Esempio 12.- Studiare la seguente funzione e accennare il grafico \[f(x)=4+e^{\sqrt{x}}-\sqrt{x}\]
Esempio 13.- Studiare la seguente funzione e accennare il grafico\[f(x)=-ln(senx)\]
Esempio 14.- Studiare la seguente funzione e accennare il grafico\[f(x)=6xe^{\frac{1}{x}}\]
Esempio 15.- Studiare la seguente funzione e accennare il grafico\[f(x)=\sqrt{x+1}-\sqrt{x}\]
Altre funzioni assegnate per l’esame di matematica alla facoltà di Economia o di Biologia, Scienze Naturali, Geologia, ecc..
Esempio 16.- Studiare le seguenti 2 funzioni \[f(x)=\left\{\begin{matrix} 4+\frac{x+e^{-\sqrt{x}}}{x} & dove\: ha \: \: significato \\ 0 & \, \: \: se\: \: x =0 \end{matrix}\right.\]
\[f(x)=-100+x^{2}e^{1-x^{2}}\]
Esempio 17.- Studiare le seguenti 6 funzioni
$y=\frac{\sqrt{x^{2}-4}}{2x-6}$, $y=e^{-x}\sqrt{x-1}$, $y=exp\left (- \frac{x^{2}}{x+2} \right )$,
$f(x)=x^{2}\left ( lnx-1 \right )$, $f(x)=\sqrt{e^{\frac{1}{ln\, x}}-1}$,
$f(x)=\frac{lnx}{1+lnx}$
Esempio 18.- Studiare le seguenti 3 funzioni \[f(x)=\left\{\begin{matrix} -4+ln\left ( \frac{\sqrt{x}-1}{x} \right ) & se\, \, x>1\\ -\left ( x-1 \right )^{2} & se\, x\leq 1 \end{matrix}\right.\]
\[f(x)=\left\{\begin{matrix} e^{-\left ( x-3 \right )^{2}} & se\, \, x\geq 3\\ -\left ( x-3 \right )^{2}-9 & se\, x < 3 \end{matrix}\right.\]
\[f(x)=\left\{\begin{matrix} \frac{e^{6x}}{\left ( e^{3x}-1 \right )^{2}} & se\, \, x\neq 0\\ -2& se\, x =0 \end{matrix}\right.\]
Esempio 19.- Studiare le seguenti 4 funzioni \[f(x)=\left\{\begin{matrix} \left ( x-lnx \right )(lnx)-x-2 & se\, \, x> 0\\ 2-x^{2}& se\, x \leq 0 \end{matrix}\right.\]
\[f(x)=\left\{\begin{matrix} 2-3lnx-x^{3}& se\, \, x> 0\\ x^{3}& se\, x \leq 0 \end{matrix}\right.\]
\[f(x)=\left\{\begin{matrix} -1+\frac{x-lnx}{x}& se\, \, x> 0\\ x+3& se\, x \leq 0 \end{matrix}\right.\]
\[f(x)=x\left ( 2+\frac{1}{lnx} \right )\]
Se non sai studiare una funzione consulta il mio libro “Lo studio di una funzione“

