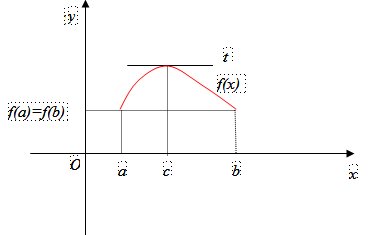
In questa pagina elenchiamo alcuni fondamentali teoremi sulle derivate.
Teorema.- Una funzione derivabile in un punto c è continua nel punto c.
Teorema di Fermat.- Se la funzione y =f(x), definita nell’intervallo [a,b], ha un massimo o minimo relativo in un punto c interno all’intervallo [a,b] e se la funzione è derivabile in c si ha che la derivata della funzione in c è nulla: $\displaystyle f'(c)=0$ . continua
Teorema di Rolle.-Sia y = f(x) una funzione definita e continua nell’intervallo chiuso [a, b], derivabile nell’intervallo aperto (a, b) e tale che f(a) = f(b), allora esiste almeno un punto c dell’intervallo aperto (a, b) tale che: \[f'(c)=0\] continua
Teorema di Lagrange.-Sia y = f(x) una funzione definita e continua nell’intervallo chiuso [a, b] e derivabile nell’intervallo aperto (a, b) allora esiste almeno un punto c dell’intervallo aperto (a, b) tale che: \[f'(c)=\frac{f(b)-f(a)}{b-a}\]
Conseguenze del teorma di Lagrange
Corollario 1.- Se una funzione ha derivata identicamente nulla nell’intervallo [a, b] allora la funzione è costante in [a, b].
Corollario 2.- Se due funzioni sono derivabili ed hanno la stessa derivata in tutti i punti di allora le due funzioni differiscono per una costate.
Corollario 3.- Se una funzione ha derivata sempre positiva in [a, b] allora è strettamente crescente in [a, b], se invece ha derivata sempre negativa in [a, b] è strettamente decrescente.
Teorema di Cauchy.- Siano y = f(x) e y = g(x) due funzioni definite e continue nell’intervallo chiuso [a, b], derivabile nell’intervallo aperto (a, b) e tale che $\displaystyle g'(x)\neq 0\, \, \, \forall x\in (a,b)$, allora esiste almeno un punto c dell’intervallo aperto (a, b) tale che:
\[\frac{f'(x)}{g'(x)}=\frac{f(b)-f(a)}{g(b)-g(a)}\]
Come conseguenza del Teorema di Cauchy si hanno i seguenti due teoremi:
1° Teorema di De L’Hôpital.- Siano y = f(x) e y = g(x) due funzioni definite nell’intervallo [a, c [, infinitesime in c $\displaystyle \left (\lim_{x\rightarrow c}f(x)=0,\, \lim_{x\rightarrow c}g(x)=0 \right )$ ed inoltre siano le due funzioni derivabili e per ogni x risulti $\displaystyle g'(x)\neq 0$. Allora se esiste il limite $\displaystyle \lim_{x\rightarrow c}\frac{f'(x)}{g'(x)}$ esiste anche il limite $\displaystyle \lim_{x\rightarrow c}\frac{f(x)}{g(x)}$ e sono uguali.
Analogo risultato vale in ]c, b]
2° Teorema di De L’Hôpital.- Siano y = f(x) e y = g(x) due funzioni definite nell’intervallo [a, c [, risulti $\displaystyle \lim_{x\rightarrow c}f(x)=\pm \infty,\, \, \lim_{x\rightarrow c}g(x)=\pm \infty$ ed inoltre siano le due funzioni derivabili e per ogni x risulti $\displaystyle g'(x)\neq 0$. Allora se esiste il limite $\displaystyle \lim_{x\rightarrow c}\frac{f'(x)}{g'(x)}$ esiste anche il limite $\displaystyle \lim_{x\rightarrow c}\frac{f(x)}{g(x)}$ e sono uguali.
Analogo risultato vale in ]c, b].
